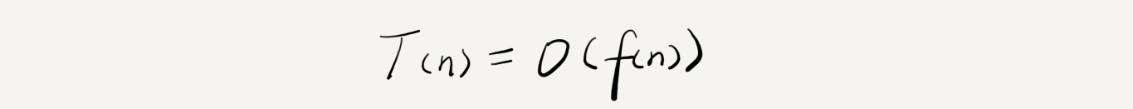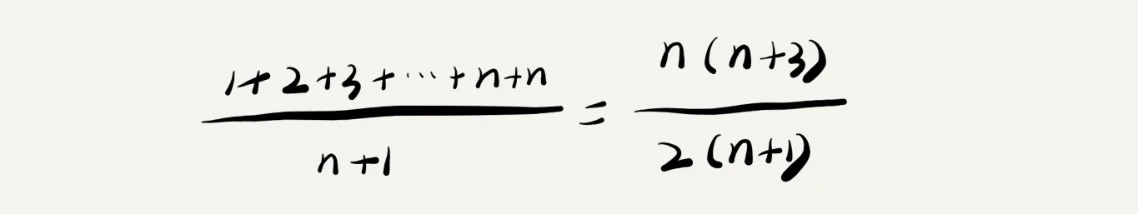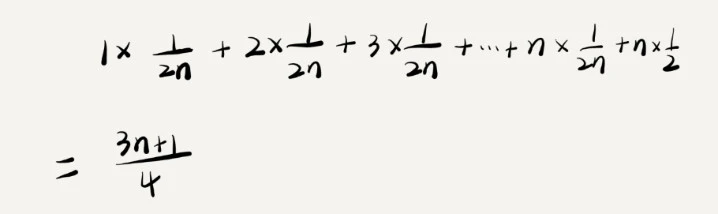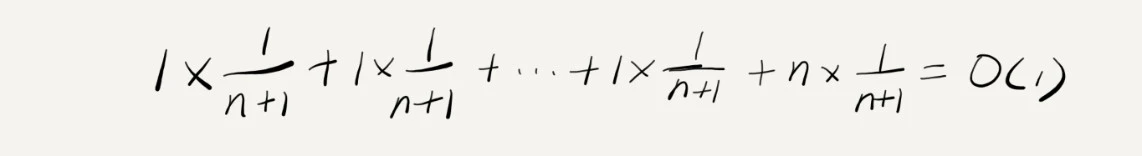第二讲

十个重点数据结构

数组
链表
栈
队列
散列表
二叉树
堆
跳表
图
Trie 树

十个重点算法

递归
排序
二分查找
搜索
哈希
贪心
分治
回溯
动态规划
字符串匹配

第三讲复杂度分析（上）

大 O 复杂度表示法

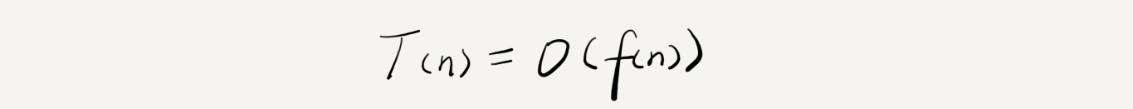
n 表示数据规模的大小
f(n) 表示每行代码执行的次数总和
T(n) 表示代码执行的时间
O 表示 T(n) 和 f(n) 成正比

大 O 时间复杂度表示的是代码执行时间随着数据规模增长的变化趋势

时间复杂度分析

三个实用分析方法

只关注循环执行次数最多的一段代码
加法法则：总复杂度等于量级最大的那段代码的复杂度
乘法法则：嵌套代码的复杂度等于嵌套内外代码复杂度的乘积

常见的时间复杂度

common_examples

空间复杂度分析

空间复杂度指算法的存储空间随着数据规模增长的变化趋势

第四讲复杂度分析（下）

时间复杂度按情况可以分为四个

最好情况时间复杂度 best case time complexity
最坏情况时间复杂度 worst case time complexity
平均情况时间复杂度 average case time complexity
均摊时间复杂度 amortized time complexity

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


// n表示数组array的长度
int find(int[] array, int n, int x) {
  int i = 0;
  int pos = -1;
  for (; i < n; ++i) {
    if (array[i] == x) {
       pos = i;
       break;
    }
  }
  return pos;
}

上述代码，最好情况是 x == array[0]，时间复杂度为 O(1) ; 最坏情况 x 不在 array 里，时间复杂度为 O(n)。

x 在数组中的位置，有 n+1中情况： 0~n-1 位置中和不在数组中。把每种情况需要遍历的元素个数相加再除以 n+1，就可以得到需要遍历的元素个数的平均值：

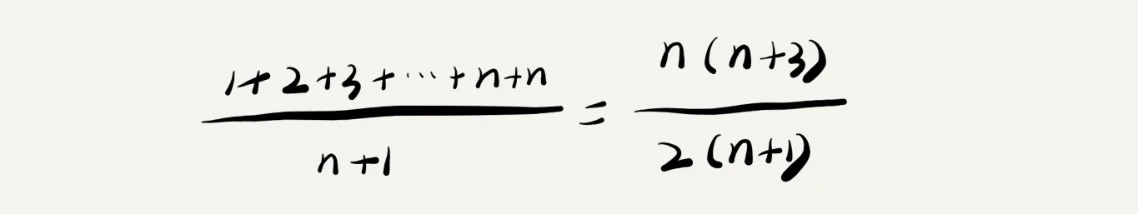
average_case

省略掉系数，常量，简化后得到复杂度为 O(n)

上面的计算方式有个问题就是没有考虑 n+1种情况出现的概率情况，不出现在数组中的概率要大于处在某个位置的概率。为了简化问题，假设出现和不出现在数组中的概率都为 1/2, 那么出现在数组中某个位置的概率为 1/2n.

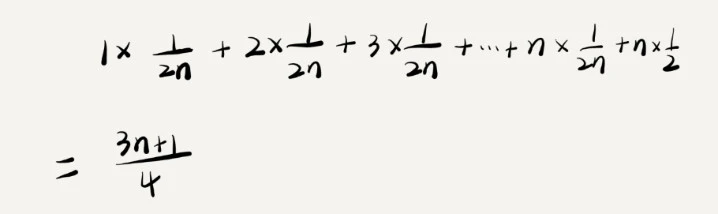
average_case2

这个值是概率论中的加权平均值，也叫期望值，所以这里的平均时间复杂度叫加权平均复杂度

省略掉系数，常量，简化后得到复杂度也为 O(n),

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18


 // array表示一个长度为n的数组
 // 代码中的array.length就等于n
 int[] array = new int[n];
 int count = 0;
 
 void insert(int val) {
    if (count == array.length) {
       int sum = 0;
       for (int i = 0; i < array.length; ++i) {
          sum = sum + array[i];
       }
       array[0] = sum;
       count = 1;
    }

    array[count] = val;
    ++count;
 }

上述代码实现了数组插入功能，如果数组没满，直接插入，如果满了，将数组求和放入第一个位置，然后将新的数据插入。

最好情况时间复杂度为 O(1), 即数组没满的时候

最坏情况时间复杂度为 O(n), 即数组满了的时候

平均情况时间复杂度为 O(1), 计算过程如下

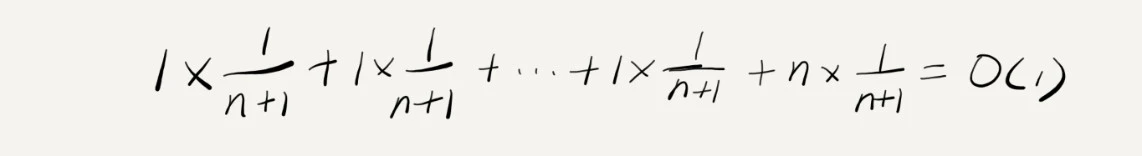
average_case3

针对示例，每次 O(n) 的插入操作，都会跟着 n-1 次 O(1) 的插入操作，那么把耗时多的一次操作均摊到接下来的耗时少的 n-1 次操作，均摊下来，这一组连续插入操作的均摊时间复杂度为 O(1).

第五讲数组

数组（Array）是一种线性表数据结构，它用一组连续的内存空间，来存储一组具有相同类型的数据。

arr_1

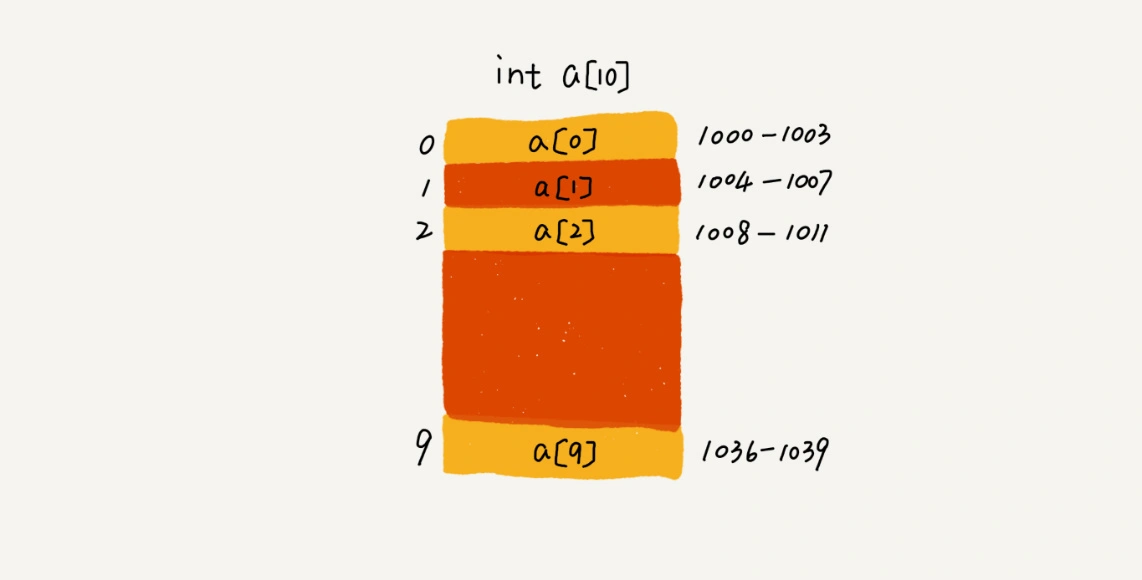
假设上图数组 a 的地址为 base_address = 1000，那么元素 a[i] 的地址为 base_address + i * data_type_size

时间复杂度

下标访问：O(1)
插入：最好 O(1), 最坏 O(n), 平均 (1+2+…+n)/n = O(n)
删除：最好 O(1), 最坏 O(n), 平均 O(n)

第六讲链表

链表通过指针将一组零散的内存块串联在一起，常见的有单向链表、双向链表和循环链表

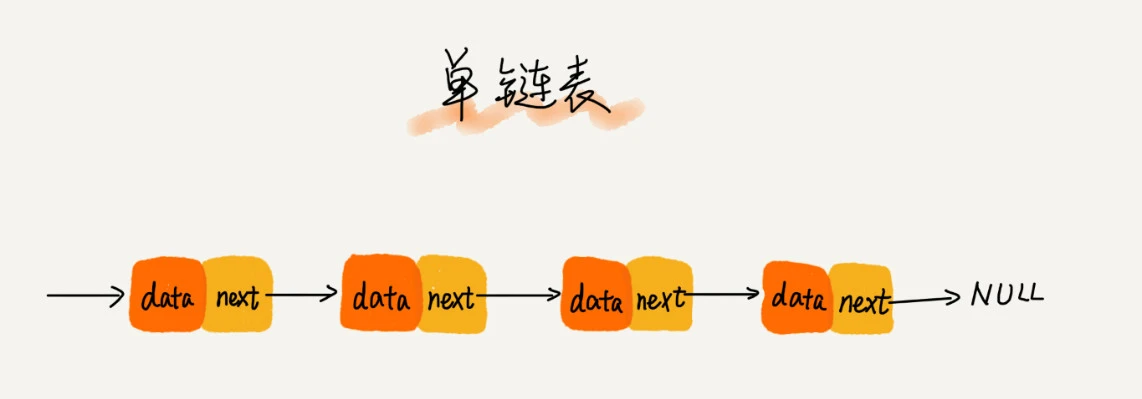
link_list

链表相比数组的优点在于插入和删除的复杂度是 O(1)

第八讲栈

栈只允许在一端插入和删除数据，并且满足先进后出的特性，入栈和出栈的复杂度为 O(1)

第九讲队列

队列和栈比较相似，只允许在一端插入，在另一端删除数据，并且满足先进先出的特性，入队和出队的复杂度为 O(1)

第十讲递归

递归问题三个前置条件

一个问题的解可以分为若干个子问题的解
该问题和子问题的求解思路完全一样
存在递归终止条件

第十一讲排序(上)

评价算法的主要维度

时间复杂度
空间复杂度，是否为原地排序
稳定性，相等元素排序前后的先后顺序是否不变

常见三种 O(n2) 复杂度排序算法详情如下

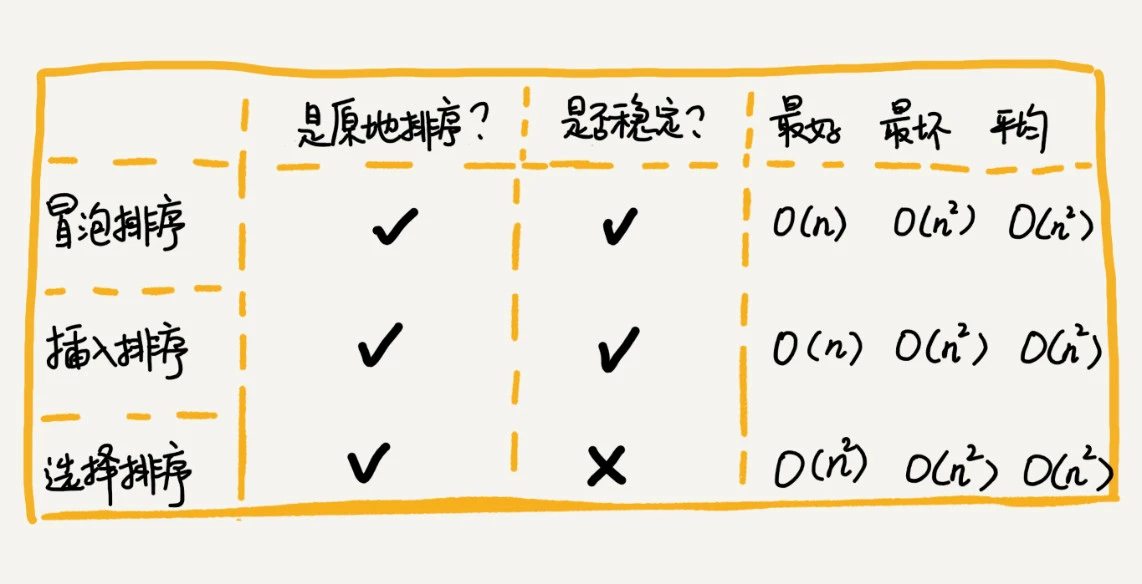
on2_sort

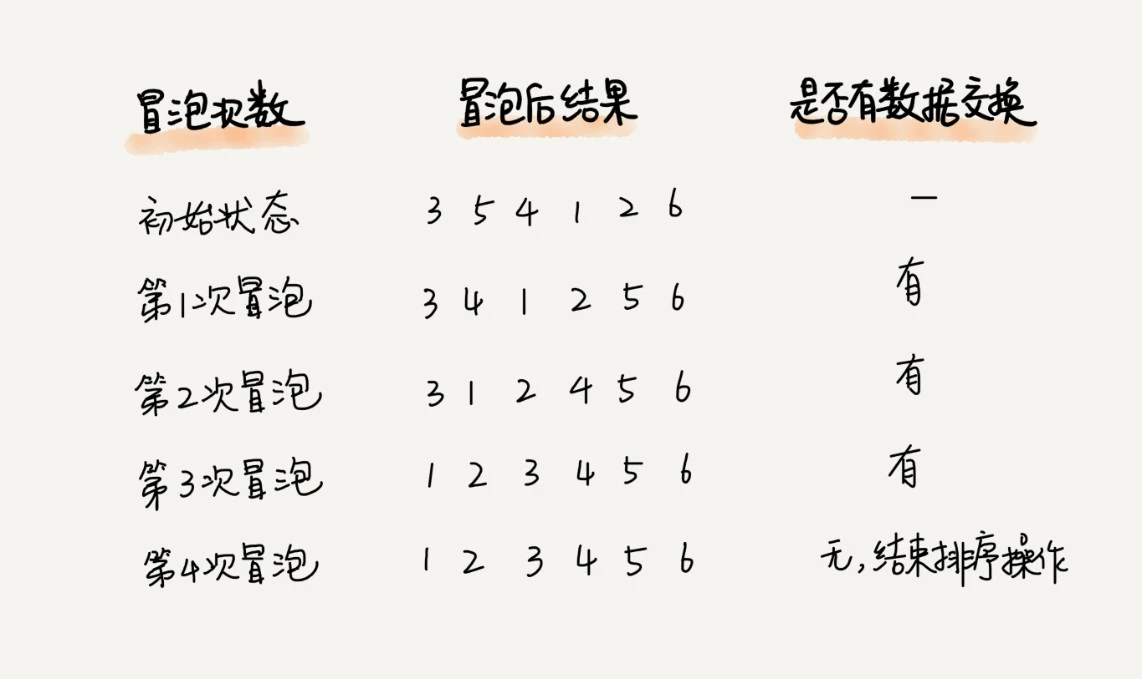
冒泡排序

bubble_sort

1
2
3
4
5
6
7
8
9


def bubble_sort(nums: list[int]):
    swapped = False
    for i in range(len(nums)-1):
        for j in range(len(nums) - 1 - i):
            if nums[j] > nums[j + 1]:
                nums[j], nums[j + 1] = nums[j + 1], nums[j]
                swapped = True
        if not swapped:
            break

冒泡排序最好的情况，数据完全有序，复杂度为 O(n)；

冒泡排序最坏的情况，数据完全逆序，复杂度为 O(n2)；

有序元素对：指对于 i, j 两个位置的元素满足 a[i] <= a[j] 且 i < j 的情况。零有序度：数据完全逆序，有序度为 0；满有序度：数据完全有序，有序度为 n*(n-1)/2。

数据的平均有序度为 (n*(n-1)/2)/2, 所以冒泡排序的平均复杂度为 O(n2)

插入排序

将数组分为两个区间

已排序区间：初始值只有一个元素，即第一个元素
未排序区间

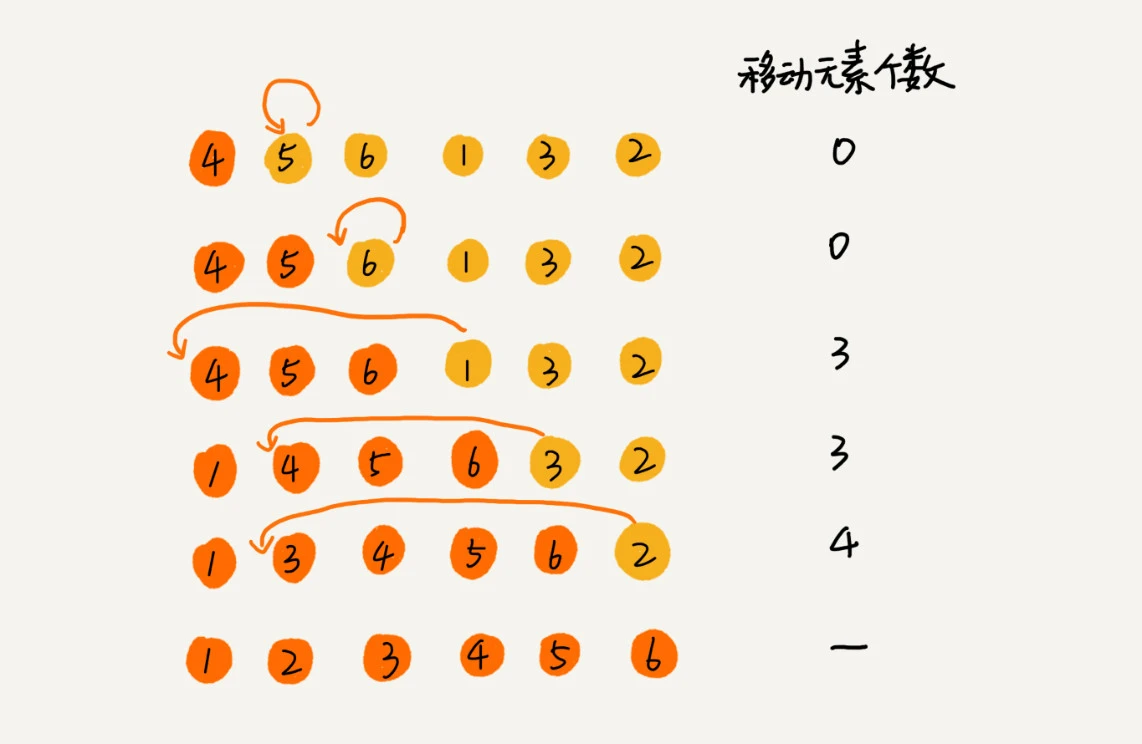
核心思想是依次取未排序区间的元素，在已排序区间找到合适的位置插入，保证已排序区间一直有序

insertion_sort

1
2
3
4
5
6
7
8


def insertion_sort(nums: list[int]):
    for i in range(1, len(nums)):
        j = i-1
        v = nums[i]
        while j >= 0 and nums[j] > v:
            nums[j+1], nums[j] = nums[j], nums[j+1]
            j -= 1
        nums[j+1] = v

插入排序最好的情况，数据完全有序，每次只要比较一个数据就能确定数据插入的位置，复杂度为 O(n)；

插入排序最坏的情况，数据完全逆序，复杂度为 O(n2)；

数组平均插入复杂度未 O(n), 所以插入排序的平均复杂度为 O(n2)

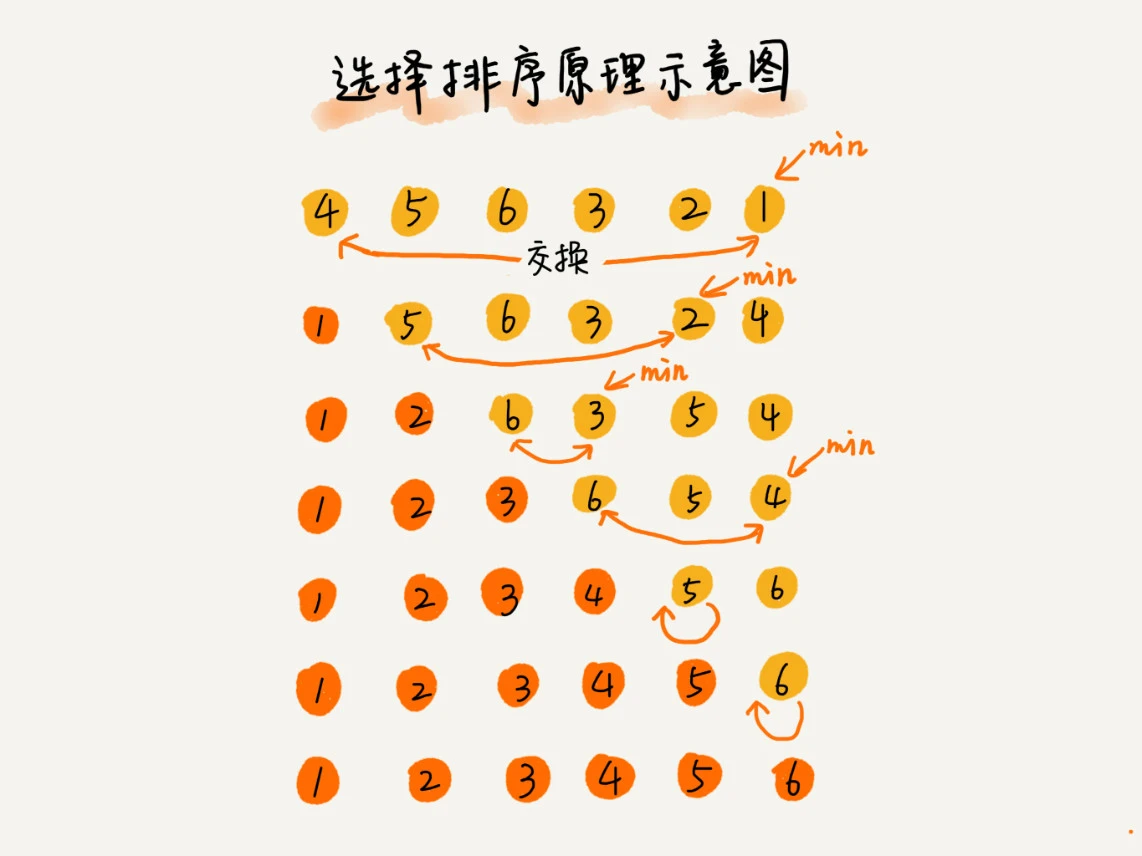
选择排序

选择排序也分为已排序区间和未排序区间，每次选择未排序区间最小元素放到已排序区间的末尾

selection_sort

1
2
3
4
5
6
7


def selection_sort(nums: list[int]):
    for i in range(len(nums)-1):
        idx = i
        for j in range(i+1, len(nums)):
            if nums[j] < nums[idx]:
                idx = j
        nums[idx], nums[i] = nums[i], nums[idx]

选择排序是不稳定的算法，如 [5, 8, 5, 2, 9]

选择排序的最好/最坏/平均复杂度都为 O(n2)

第十二讲排序(下)

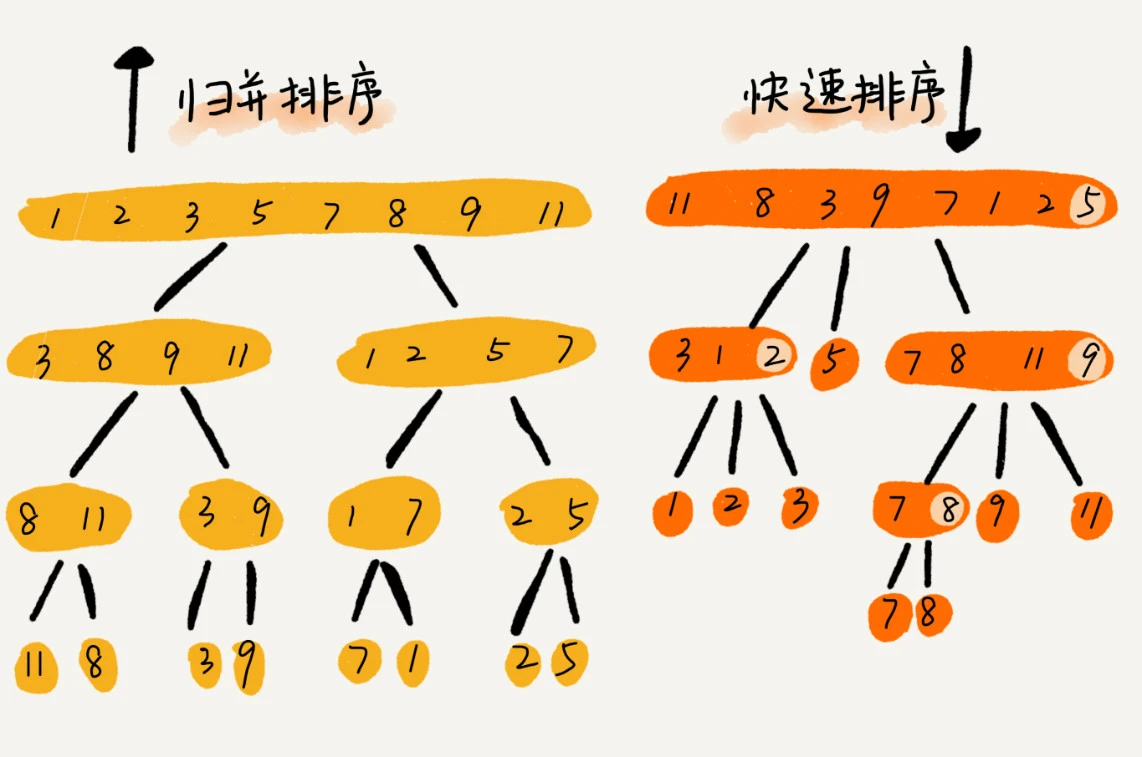
dividend_sort

归并排序

归并排序利用分治的思想，并用递归的技巧来实现

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25


def merge(left, right) -> list[int]:
    i, j = 0, 0
    res = []

    while i < len(left) and j < len(right):
        if left[i] < right[j]:
            res.append(left[i])
            i += 1
        else:
            res.append(right[j])
            j += 1
    while i < len(left):
        res.append(left[i])
        i += 1
    while j < len(right):
        res.append(right[j])
        j += 1
    return res


def merge_sort(nums: list[int]) -> list[int]:
    if len(nums) < 2:
        return nums
    mid = len(nums) // 2
    return merge(merge_sort(nums[:mid]), merge_sort(nums[mid:]))

归并排序的空间复杂度未 O(n) (临时空间使用后就释放了)

归并排序的最好/最坏/平均复杂度都为 O(nlogn)

快速排序

快速排序是不稳定的排序算法

归并排序平均复杂度都为 O(nlogn), 但极极端情况可能退化未 O(n2), 比如数组本身有序，又选择最后一个元素作为 pivot 的情况

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20


def partition(nums: list[int], l: int, r: int) -> int:
    pivot = nums[r]
    i = l
    for j in range(i, r):
        if nums[j] < pivot:
            nums[j], nums[i] = nums[i], nums[j]
            i += 1
    nums[i], nums[r] = nums[r], nums[i]
    return i

def _quick_sort(nums: list[int], l: int, r: int):
    if l >= r:
        return
    idx = partition(nums, l, r)
    _quick_sort(nums, l, idx-1)
    _quick_sort(nums, idx+1, r)


def quick_sort(nums: list[int]):
    _quick_sort(nums, 0, len(nums)-1)

第十三讲线性排序

桶排序（Bucket Sort）

bucket_sort

假设有 n 个数据，均匀地分布到 m 个桶内，每个桶内有 k = n/m 个元素，每个桶使用快排排序，复杂度为 O(klogk)，总复杂度为 O(nlog(n/m))，当 m 接近 n 时，log(n/m) 是个非常小的常量，所以复杂度接近 O(n)

桶排序的前提条件是数据能均匀分布在每个桶中，并且桶与桶之间有大小顺序。极端情况如果数据分布在一个桶中，复杂度退化为 O(nlogn)

桶排序适合外部排序

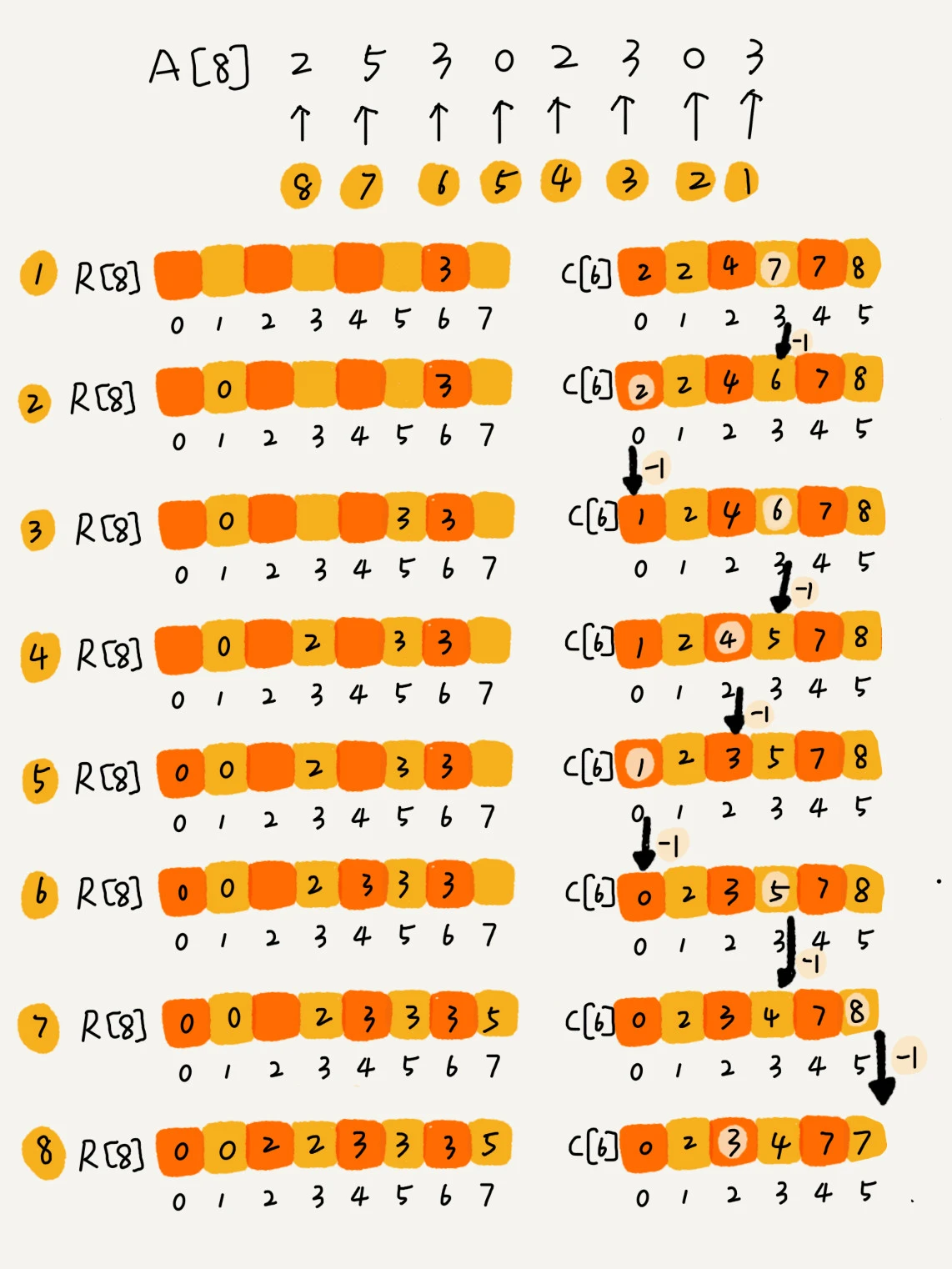
计数排序（Counting Sort）

计数排序是一种特殊的桶排序，相当于每个桶中的数据都是相同的值。

counting_sort

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19


def counting_sort(nums: list[int]):
    m = max(nums)

    c = [0 for _ in range(m + 1)]

    for num in nums:
        c[num] += 1

    for i in range(1, m + 1):
        c[i] += c[i - 1]

    r = [0 for _ in range(len(nums))]
    for i in range(len(nums) - 1, -1, -1):
        idx = c[nums[i]] - 1
        r[idx] = nums[i]
        c[nums[i]] -= 1

    for i in range(len(nums)):
        nums[i] = r[i]

计数排序适用于数据范围不大的非负整数的场合

基数排序（Radix Sort）

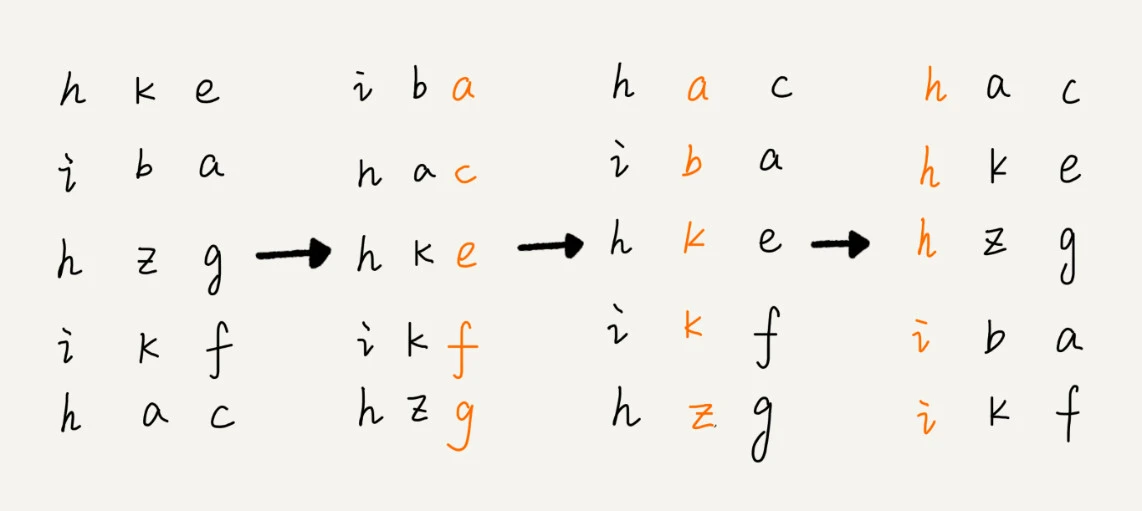
radix_sort

基数排序要求数据可以分割出独立的位来比较，且位的范围不大

第十四讲快速排序优化

优化分区点

如果数组原本就是有序的，且分区点都取最后一个，这样复杂度就会退化到 O(n2)。

有两种简单的优化方式

三数取中法：从区间前中后取三个数，比较大小选中间的那个
随机法

glibc qsort 的优化方式

数据量不大的时候使用归并排序
使用三数取中法
快排区间小于4时使用插入排序，并使用哨兵机制来优化
在堆上实现栈，避免过深的递归导致栈溢出

第十五讲二分查找

二分查找的依赖条件是：数据有序且可以随机访问

对于不存在重复元素的解法：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


def binary_search(nums: list[int], v: int) -> int:
    l, r = 0, len(nums)-1

    while l <= r:
        m = (l+r)//2
        if nums[m] == v:
            return m
        elif nums[m] < v:
            l = m+1
        else:
            r = m-1
    return -1

存在重复元素的第一个值：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


def binary_search(nums: list[int], v: int) -> int:
    l, r = 0, len(nums)-1

    while l <= r:
        m = (l+r)//2
        if nums[m] == v:
            if m == 0 or nums[m-1] != v:
                return m
            else:
                r = m - 1
        elif nums[m] < v:
            l = m+1
        else:
            r = m-1
    return -1

存在重复元素的最后一个值：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


def binary_search(nums: list[int], v: int) -> int:
    l, r = 0, len(nums)-1

    while l <= r:
        m = (l+r)//2
        if nums[m] == v:
            if m == len(nums)-1 or nums[m+1] != v:
                return m
            else:
                l = m + 1
        elif nums[m] < v:
            l = m+1
        else:
            r = m-1
    return -1 

存在重复元素的大于等于的第一个值：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


def binary_search(nums: list[int], v: int) -> int:
    l, r = 0, len(nums)-1

    while l <= r:
        m = (l+r)//2
        if nums[m] >= v:
            if m == 0 or nums[m-1] < v:
                return m
            else:
                r = m - 1
        else:
            l = m+1
    return -1

存在重复元素的小于等于的最后一个值：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


def binary_search(nums: list[int], v: int) -> int:
    l, r = 0, len(nums)-1

    while l <= r:
        m = (l+r)//2
        if nums[m] <= v:
            if m == len(nums)-1 or nums[m+1] > v:
                return m
            else:
                l = m + 1
        else:
            r = m-1
    return -1

第十七章跳表

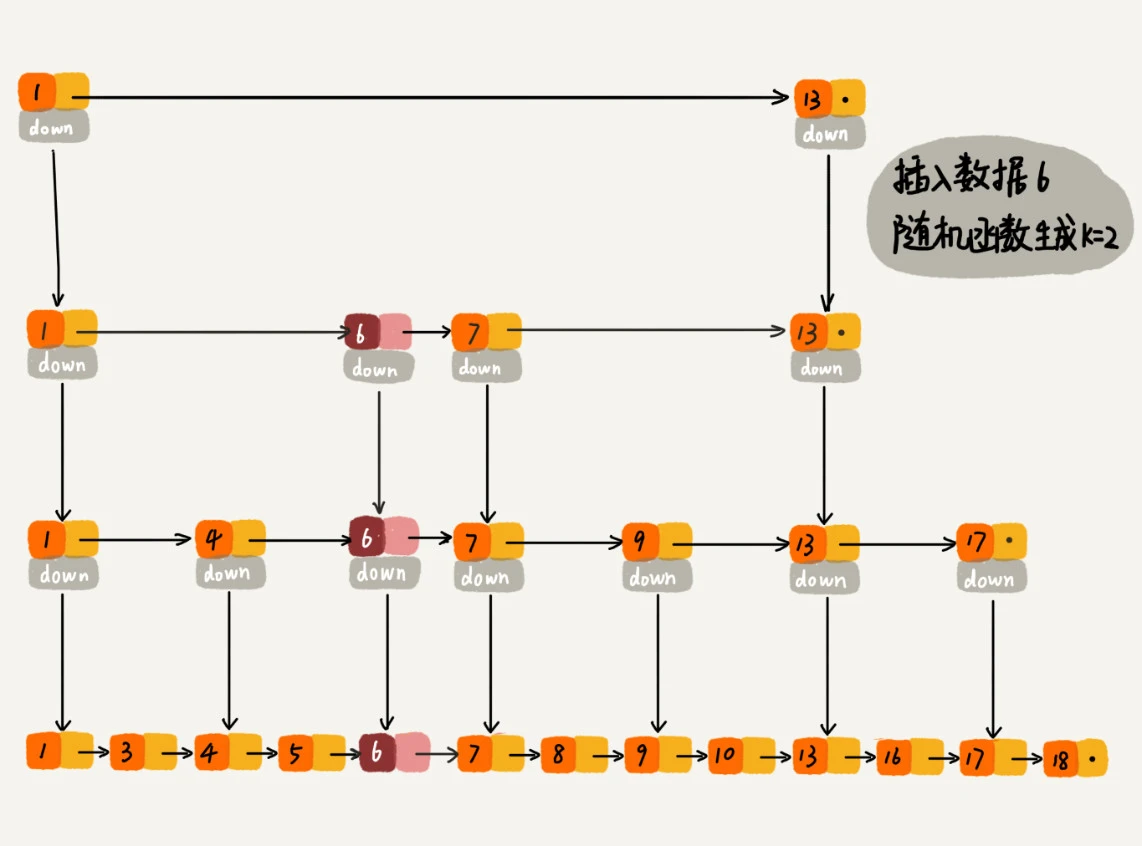
skip_list

通过给链表添加索引，这样就可以实现快速增删查

通过随机函数确定插入在哪一层

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


// https://github.com/MauriceGit/skiplist
func (t *SkipList) generateLevel(maxLevel int) int {
	level := maxLevel - 1
	// First we apply some mask which makes sure that we don't get a level
	// above our desired level. Then we find the first set bit.
	var x uint64 = rand.Uint64() & ((1 << uint(maxLevel-1)) - 1)
	zeroes := bits.TrailingZeros64(x)
	if zeroes <= maxLevel {
		level = zeroes
	}

	return level
}

redis 作者回答 zset 选用跳表的理由：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


// https://news.ycombinator.com/item?id=1171423

antirez on March 6, 2010 | root | parent | next [–]
 
There are a few reasons:
1) They are not very memory intensive. It's up to you basically. Changing parameters about the probability of a node to have a given number of levels will make then less memory intensive than btrees.

2) A sorted set is often target of many ZRANGE or ZREVRANGE operations, that is, traversing the skip list as a linked list. With this operation the cache locality of skip lists is at least as good as with other kind of balanced trees.

3) They are simpler to implement, debug, and so forth. For instance thanks to the skip list simplicity I received a patch (already in Redis master) with augmented skip lists implementing ZRANK in O(log(N)). It required little changes to the code.

第十八章散列表（上）

散列表是基于数组的随机访问特性，利用散列函数，将数据映射到数组的某个位置

散列冲突

常用的解放方案有开放寻址法（open addressing）和链表法（chaining）

开放寻址法

最简单的一种开放寻址法为线性探测：如果位置被占用，会继续寻找。

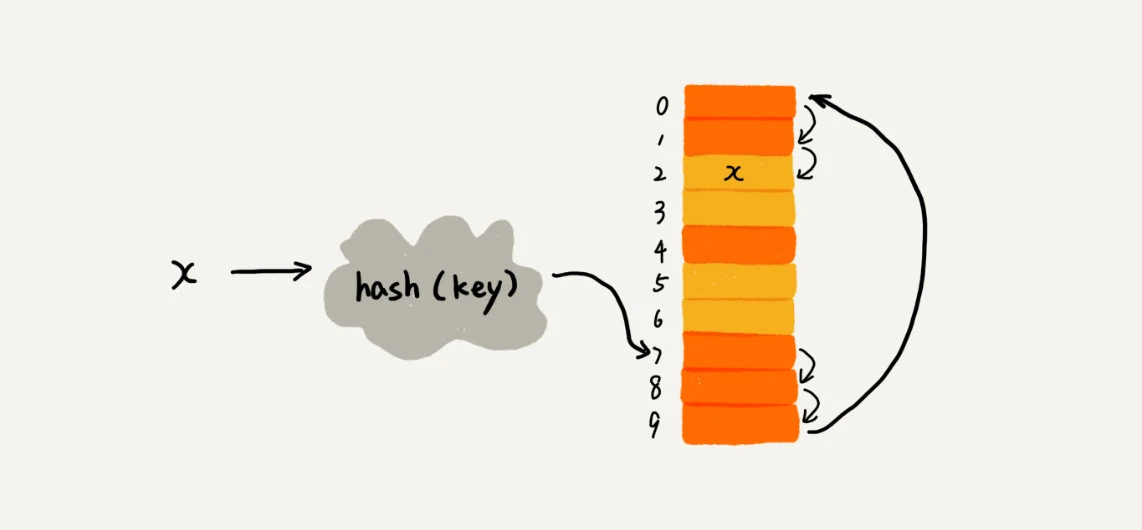
linear_probing

二次探测 quadratic probing: 步长变为步数的平方，如 hash(x) + 0、 hash(x) + 1^2、hash(x) + 2^2 双重散列 double hashing: 使用多个散列函数，第一个发现占用后，使用第二个

链表法

链表法将散列值相同的数据放在同一个链表中

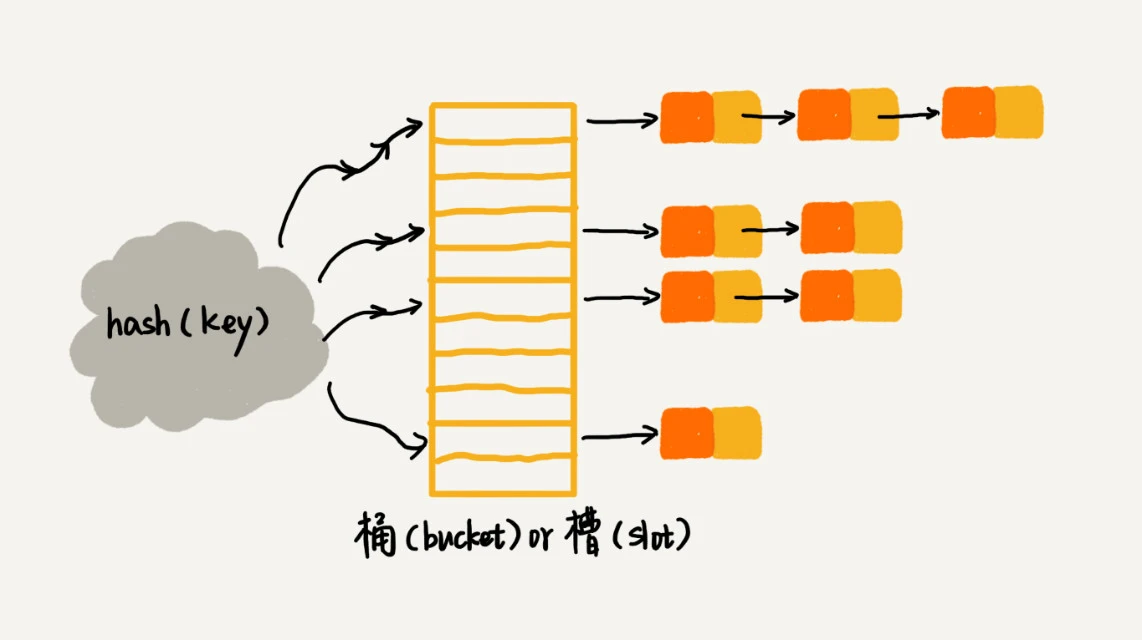
chaining

查找和删除的复杂度和链表长度 k 成正比，即 O(k)

第十九章散列表（中）

哈希函数设计

不过太耗时
尽可能随机且随机分布

扩容

扩容时，只申请空间，不搬迁数据。

当插入数据时，将数据插入新的表，并搬迁一个旧表的值到新表
查询数据时，先查新表，没查到再查旧表

increase_capacity

Java HashMap 实现优化

采用链表法解决冲突，链表长度超过8时改用红黑树

第二十一讲哈希算法（上）

定义

将任意长度的二进制值串映射为固定长度的二进制值串的规则称为哈希算法。

优秀哈希算法要求

单向，不可从哈希值推导出原始值
对数据敏感，差了一个 bit 的两个数据的哈希值大不相同
冲突概率非常小
执行效率高效

应用场景

安全加密，md5 哈希值有 2^128 种可能
唯一标识
数据校验
散列函数

第二十二讲哈希算法在分布式服务中的应用

负载均衡

对客户端会话ID 或者 IP 地址计算哈希值，然后对服务器列表大小进行取余，得到列表索引位置。

数据分片

分布式存储

一致性哈希算法示例： GeeCache一致性哈希

第二十三章二叉树

树的相关概念

根节点：没有父节点的节点叶子节点：没有子节点的节点

高度、深度和层的示意如下图

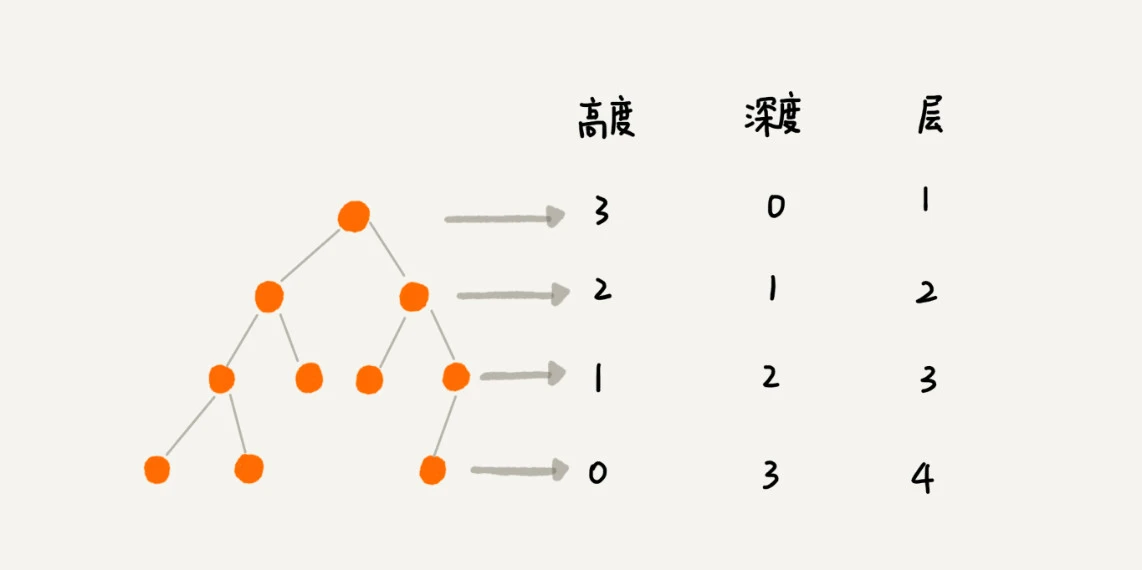
height_depth_level

二叉树

完全二叉树：叶子节点都在最后两层，最后一层的叶子节点都靠左排列，除了最后一层，其他层节点的个数要达到最大

满二叉树：叶子节点都在最后一层，除了叶子节点之外，每个节点都有两个子节点

链式存储方式

使用链表来存储，每个节点有三个字段，一个字段存储数据，另外两个字段分别指向左右子节点

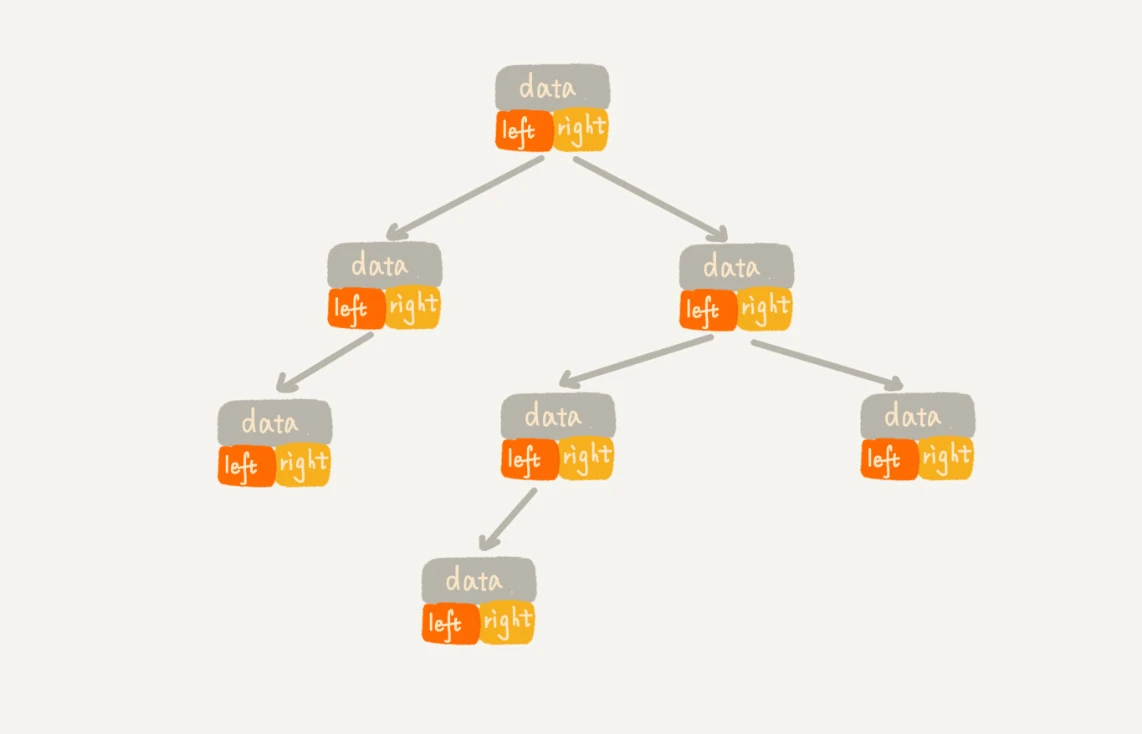
link_tree

顺序存储方式

根节点存储下标为 1 的位置，左节点存在下标为 2i 的位置，右节点存储在 2i+1 的位置

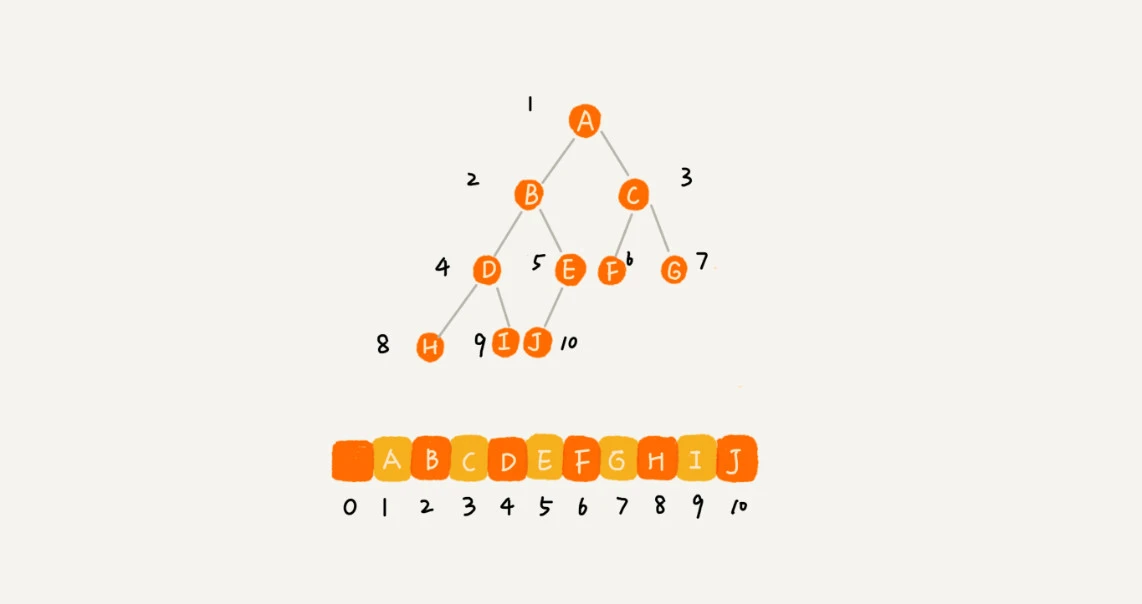
arr_tree

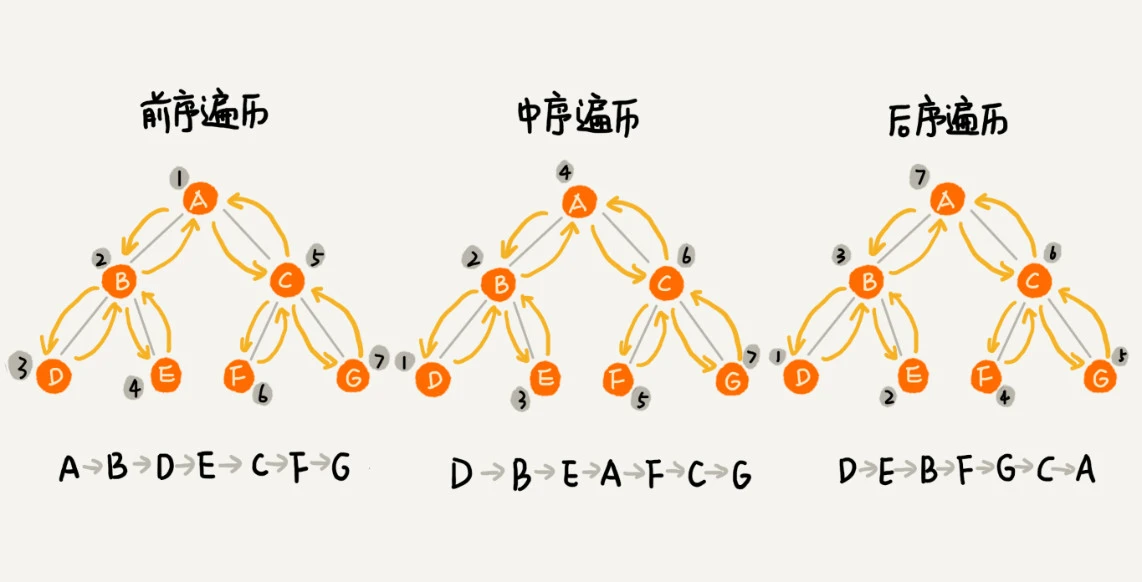
遍历

二叉树有三种经典的遍历方式：前序遍历、中序遍历、后续遍历

tree_traversal

第二十四章二叉查找树

二叉查找树：对于任意一个节点，其左子树的每个节点均小于它，右子树的每个节点都大于它

查找操作

从根节点出发，如果等于要找的数据则返回，如果小于则从左子树找，否则从右子树找。

插入操作

从根节点出发，如果大于根节点，当右节点为空，则直接插到右节点的位置，否则遍历右子树；如果小于根节点，当左节点为空，则直接插到左节点的位置，否则遍历左子树。

删除操作

当目标节点没有子节点，将其父节点指向的指针置为空
当目标节点有一个子节点，将其父节点指向的指针指向目标节点的子节点
当目标节点有两个子节点，用目标节点右子树的最小节点来替换目标节点

第二十五章平衡二叉查找树

极端情况下二叉查找树会退化成链表，所以需要设计平衡二叉树来避免性能退化的问题。

平衡二叉树的严格定义：任何一个节点的左右子树的高度差值不能大于一。

AVL 树完全满足平衡二叉树的严格定义，查找效率高，但为了维持这种高度的平衡，每次插入和删除都要调整，比较复杂和耗时。

红黑树只做到了近似平衡，在维护平衡的成本上，比 AVL 树的成本低。所以查找、插入和删除操作的性能都比较稳定

红黑树中有两种颜色的节点：黑色、红色，节点具有有如如下要求：

根节点是黑色的
每个叶子节点都是黑色的空节点
相邻节点不能同时为红色，即红色节点被黑色隔开
每个节点，其到达叶子节点的所有路径中黑色节点的数量是一样的

Table of Contents

第二讲