第零讲 git diff 文本差分算法
定义
git diff 内置了多种算法 ,这里介绍的是其默认算法 Myers 差分算法。
An edit script for A and B is a set of insertion and deletion commands that transform
A into B.
文本差分算法可以定义为用于求输入源文本到目标文本之间的编辑脚本算法。
编辑脚本是其中一系列插入和删除操作的序列
评价指标
有两个指标可以评价编辑脚本的优劣,分别是编辑脚本的长度、可读性
编辑脚本长度
编辑脚本较短时,尽可能的保留了更多原序列中的元素。
最短编辑脚本(SES Shortest Edit Script)和 最长公共子序列问题其实是对偶问题
1
2
3
4
5
6
7
|
源序列
S = ABCABBA length m = 7
目标序列
T = CBABAC length n = 6
最长公共子序列(不唯一)
C = CBBA length LC = 4
|
从上面的例子可以看出 SES 的长度等于 m + n - 2 * LC
可读性
可读性可以总结为两点:
- 尽可能保留整段文本,尽可能连续删除和插入,而不是彼此交叉
- 大部分人习惯先看到原文本删除,再看到目标文本的插入
所以总结算法逻辑就是:在最短的编辑脚本里,尽量找到删除在增加前面,且尽可能多的连续删除更多行的方式。
模型抽象
从源序列 S 到目标序列 T,有删除和插入两种操作,我们需要找到一种对这两个操作和相应变换状态的抽象方式。
1
2
3
4
|
源序列
S = ABCABBA length m = 7
目标序列
T = CBABAC length n = 6
|
转化成图搜索问题
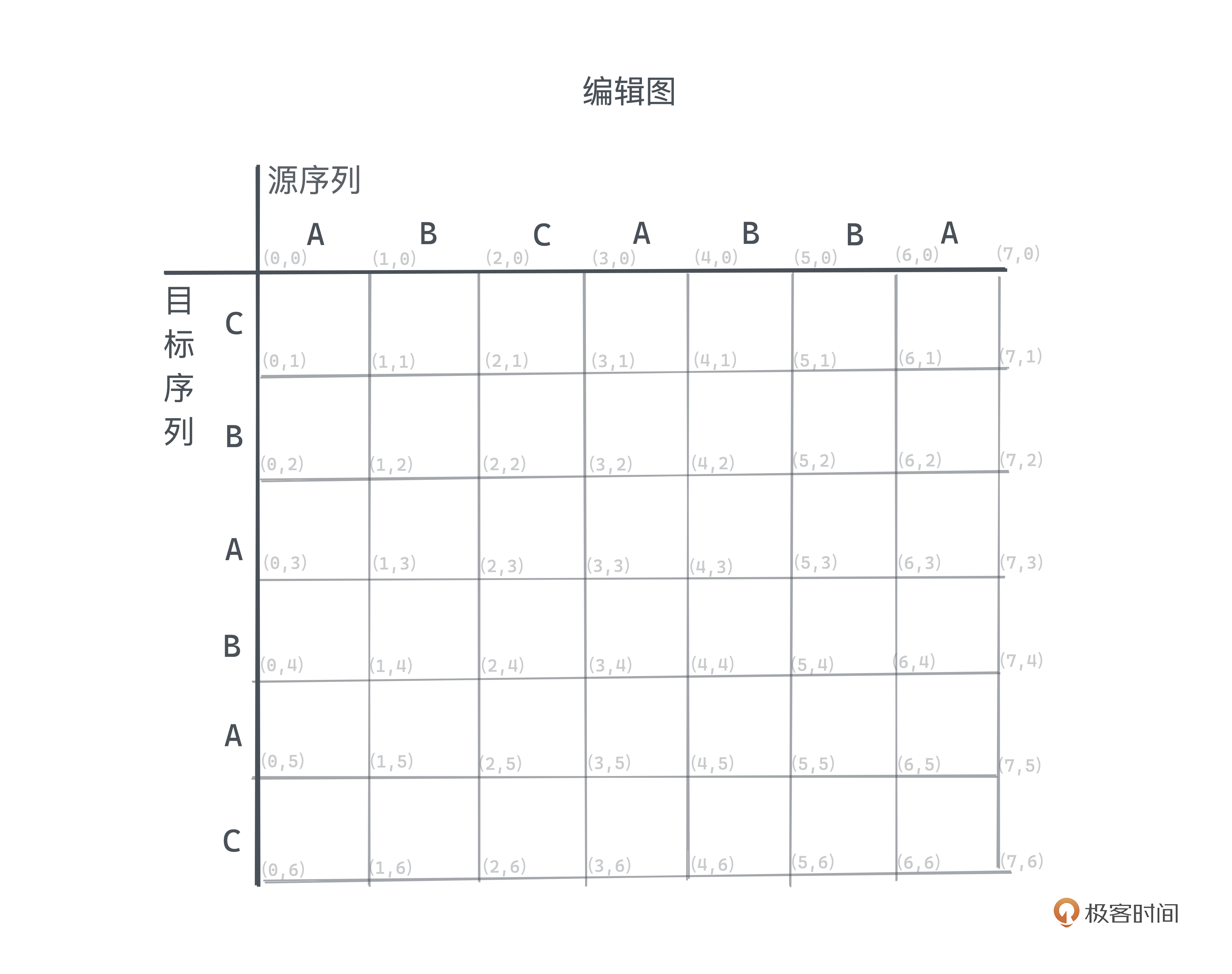
Myers 将问题转化为图搜索问题 ,其中横轴代表源序列,纵轴代表目标序列,
坐标 (0, 0) 代表初始状态,(m, n) 则对应了最终完整的从 S 到 T 的 编辑脚本 。
横向移动代表删除操作,纵向移动代表插入操作。
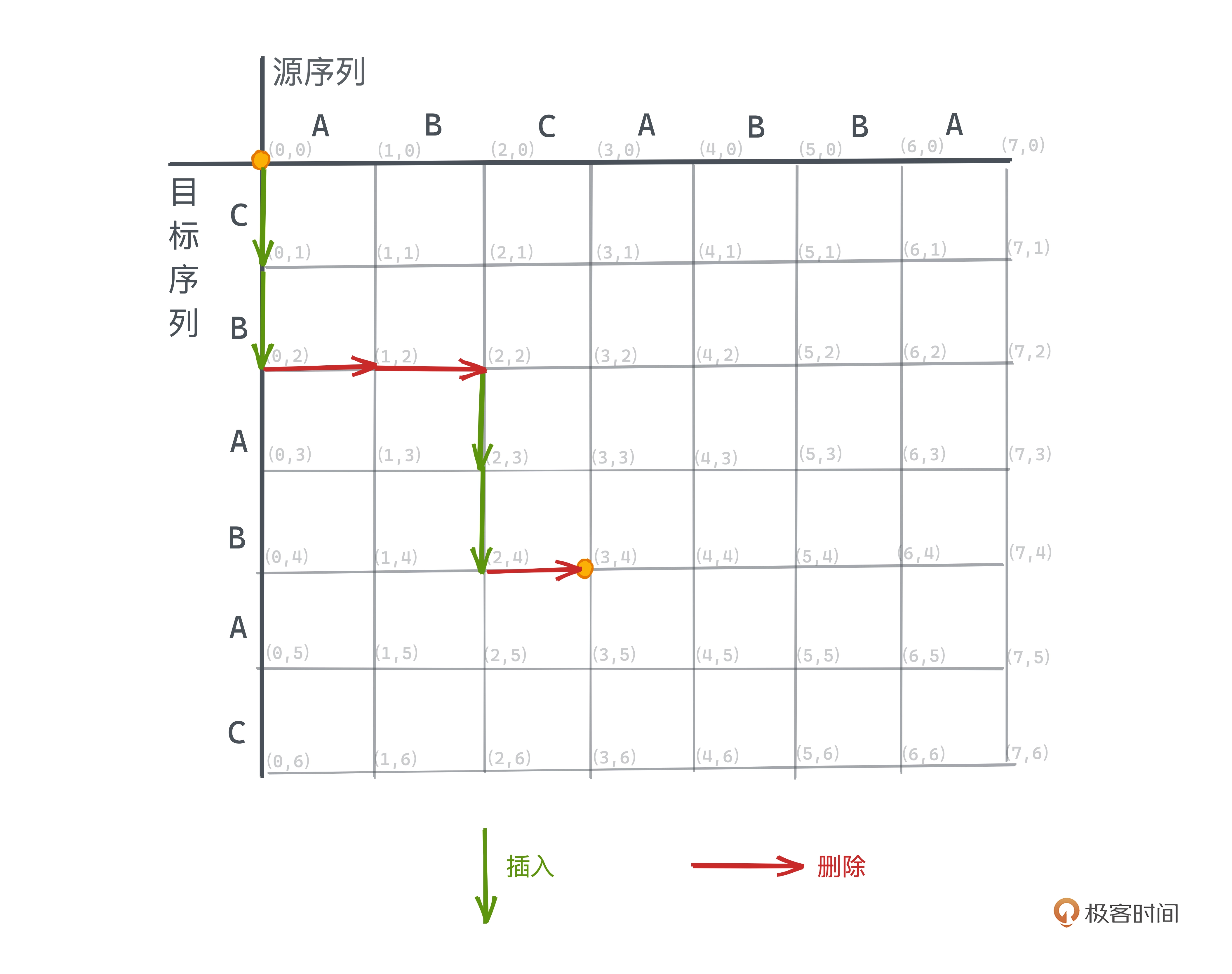
如上图所示,从 (0, 0) 到 (3,4) 的路径表示字符串 ABC –> CBAB 的一种编辑方式,
我们先插入 CB,然后删除 AB,再插入 AB,最后删除 C。
这样文本差分问题就转化成了如何在这样的网格中找到仅允许向下和向右移动的一个从
(0, 0) 到 (m, n) 的路径,路径的长度就代表了总共需要的操作数。
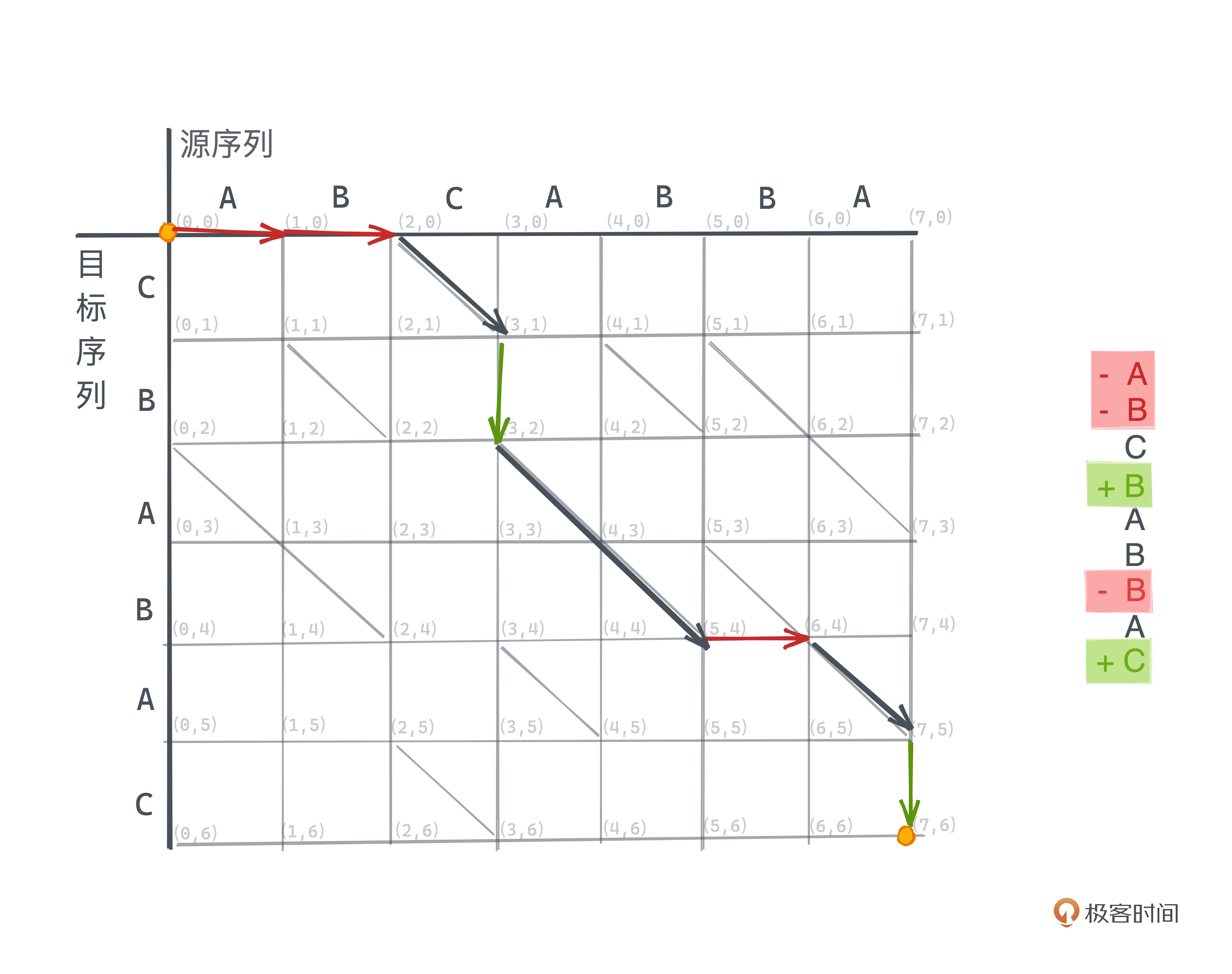
对于源序列和目标序列字符相等的坐标,如 (2, 0) 和 (3, 1)、(0, 2) 和 (2,4) 等,
这种斜线路径不耗费任何操作数。如下图为一条最短路径的例子:
如何解决图搜索
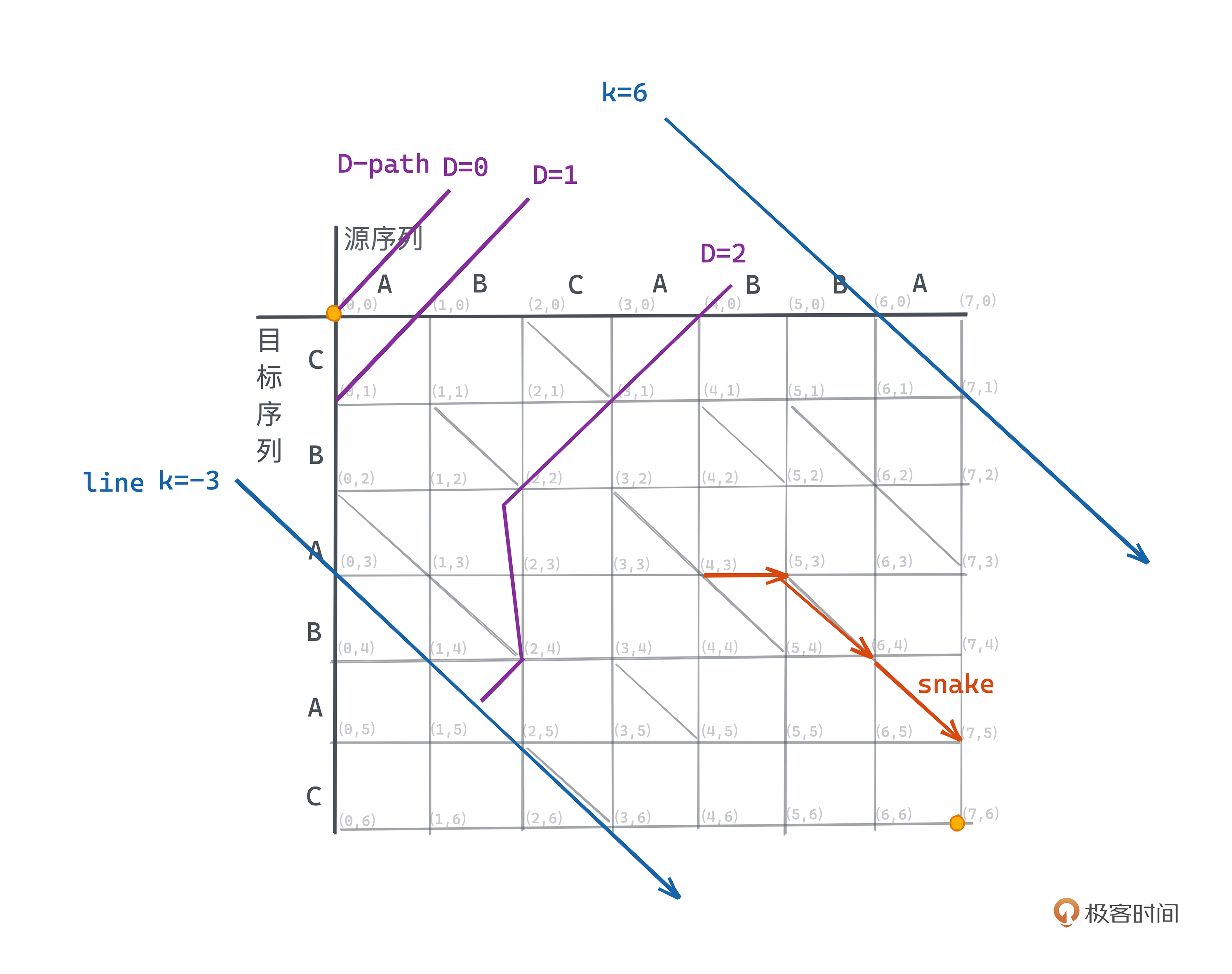
Myers 论文中有几个重要的概念
- D-path: 需要 D 步操作的路径称之为 D-Path
- snake: 一个横线或竖线之后紧跟着 n 条斜线所形成的的路径为 snake,snake 操作数为 1,且 snake 结尾坐标后继不能为斜线。
- line: 从左上到右下的 45 度的斜线,可以用 k = x - y 表示, 在 m * n 的网格中,k 的取值范围为 [-n, m]。
Myers 论文中原图对上面的几个概念示意:
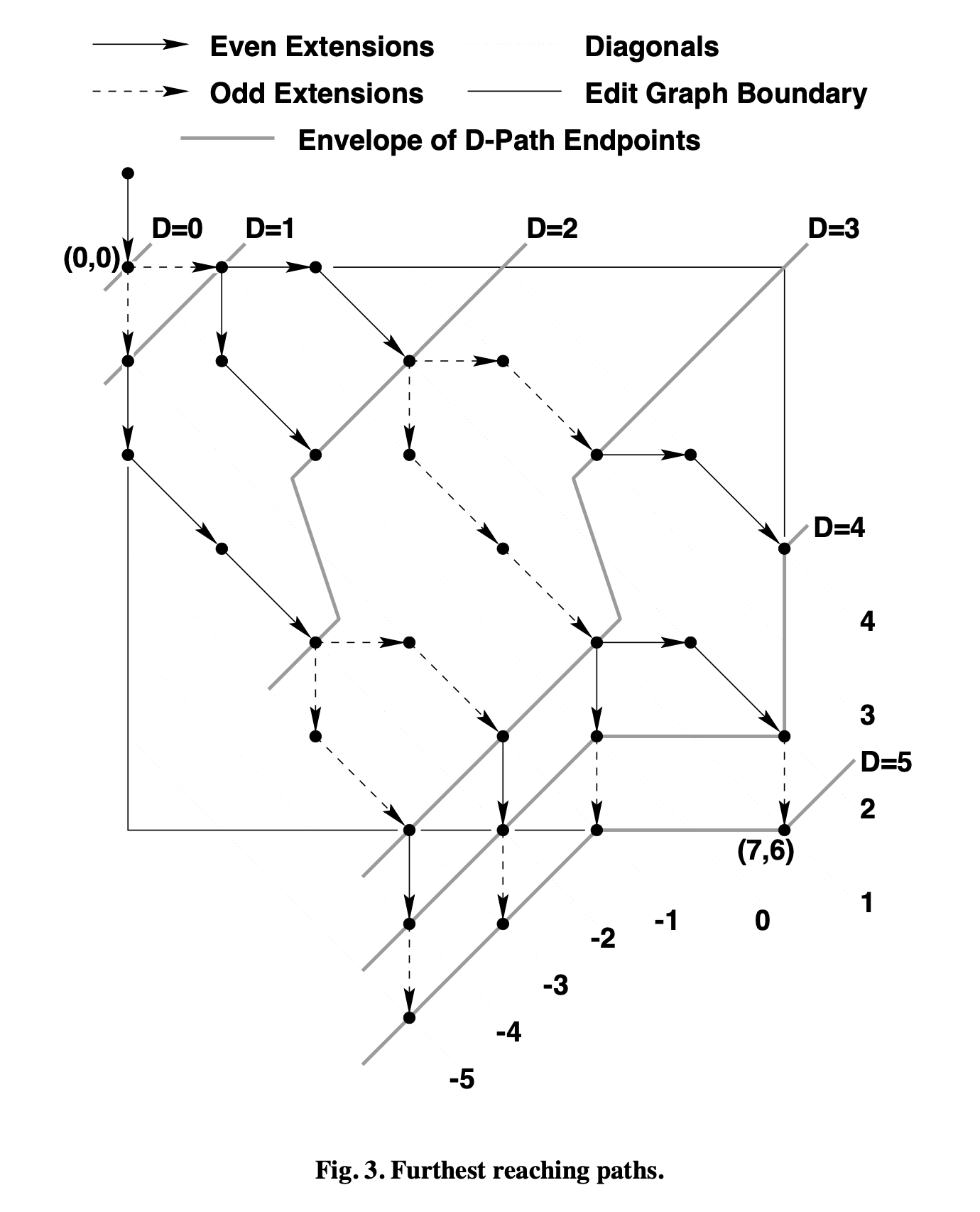
这样我们求解最短编辑脚本的目标就可以定义为找最短到达 (m, n) 的 D-path。
所有的 D-path 都是 (D-1)-path 加一条 snake 构成,这样我们可以从 1-path 出发,
去搜索所有 2-path 最远能走到哪,然后一直递推到 D-path,第一次遇到终点时,就找到最短路径了。
当有多条 D-path 时,我们如何选可读性最好的路径呢?
基于先看到删除再看到插入的原则,在考虑 D-path时,会从多条 (D-1)-path 中选出横坐标更大的路径。
代码实现
我们使用一个二维数组 dp 来记录图上的搜索状态
- dp 第一个维度代表操作数,最大操作范围是我们最短编辑脚本的长度 m + n - 2 * LC
- dp 第二个维度代表 k-line 的行号,在 操作数为 d 时, 其取值范围是 [-d, d]
- dp 的值代表对应的 x 坐标 (相应可以推算出 y 坐标)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
| 0 1 2 3 4 5
----+--------------------------------------
|
4 | 7,3
| /
3 | 5,2
| /
2 | [3,1] [7,5]
| / \ / \
1 | [1,0] [5,4] [7,6]
| / \ \
0 | [0,0] 2,2 5,5
| \ \
-1 | 0,1 4,5 5,6
| \ / \
-2 | 2,4 4,6
| \
-3 | 3,6
|
操作数为 d,行号为 k 的状态只能从相邻的两行 k-1 横线过来(x+1)或者 k+1 竖线过来(x不变)。
因为整个数的结构是二叉的 ,奇数步数时必然处于奇数行号,偶数步数时必然处于偶数行号,
这是因为每进行一步 snake 时,只会有一次删除或插入操作,所以 k 的遍历步长是 2 。
状态转移方程就是 dp[d][k] = max(dp[d-1][k-1]+1, dp[d-1][k+1]),即多个路径状选横坐标 x 最大的。
由于操作数 d 的状态计算只依赖 d-1 的状态数组,所以可以压缩一下空间使用一维数组记录即可。
伪代码
1
2
3
4
5
6
7
8
9
10
11
12
13
|
V[1]←0
For D ← 0 to MAX Do
For k ← −D to D in steps of 2
Do If k=−D or k≠D and V[k−1] < V[k+1] Then
x ← V[k+1]
Else
x ← V[k−1]+1 y ← x−k
While x < N and y < M and a[x+1] = b[y+1] Do
(x,y) ← (x+1,y+1)
V[k] ← x
If x ≥ N and y ≥ M Then
Length of an SES is D
Stop
|
python 版代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
def git_diff(a: str, b: str) -> int:
a = " " + a
b = " " + b
v = {0: 0}
d = 0
break_out = False
while True:
d += 1
for k in range(-d, d+1, 2):
if k == -d:
x = v[k + 1]
elif k == d:
x = v[k - 1] + 1
else:
if k+1 not in v:
x = v[k - 1] + 1
else:
x = max(v[k + 1], v[k - 1] + 1)
y = x - k
while x < len(a) - 1 and y < len(b) - 1 and a[x + 1] == b[y + 1]:
x += 1
y += 1
v[k] = x
if x >= len(a) - 1 and y >= len(b) - 1:
break_out = True
break
v = {k: x for k, x in v.items() if (k+d) % 2 == 0}
if break_out:
break
return d
|
第一讲 动态数组 vector
数组与内存
静态数组是由相同类型的元素线性排列的数据结构,在计算机上会分配一段连续的内存,
对元素进行顺序存储。
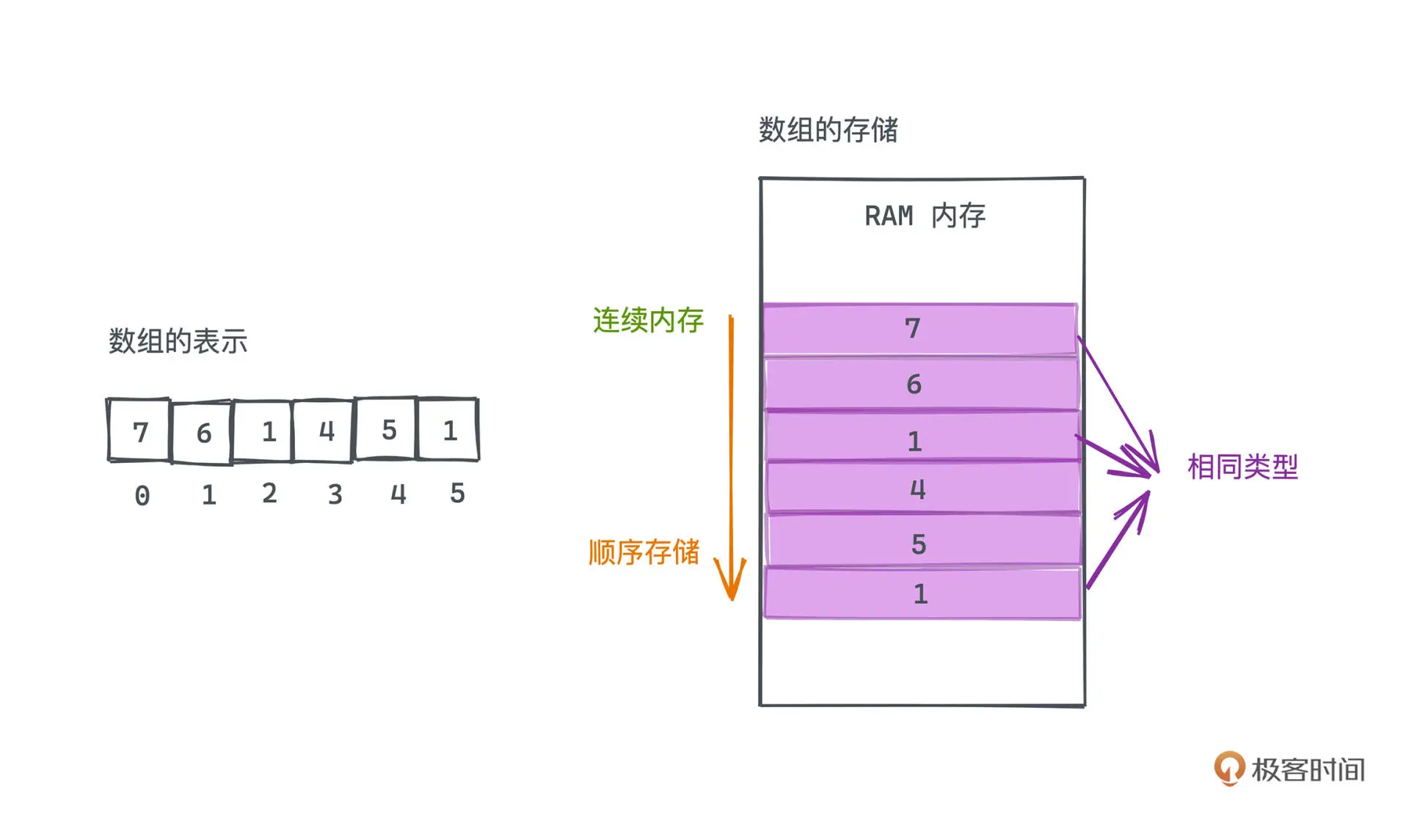
静态数组的插入和 删除的平均复杂度是 O(N)
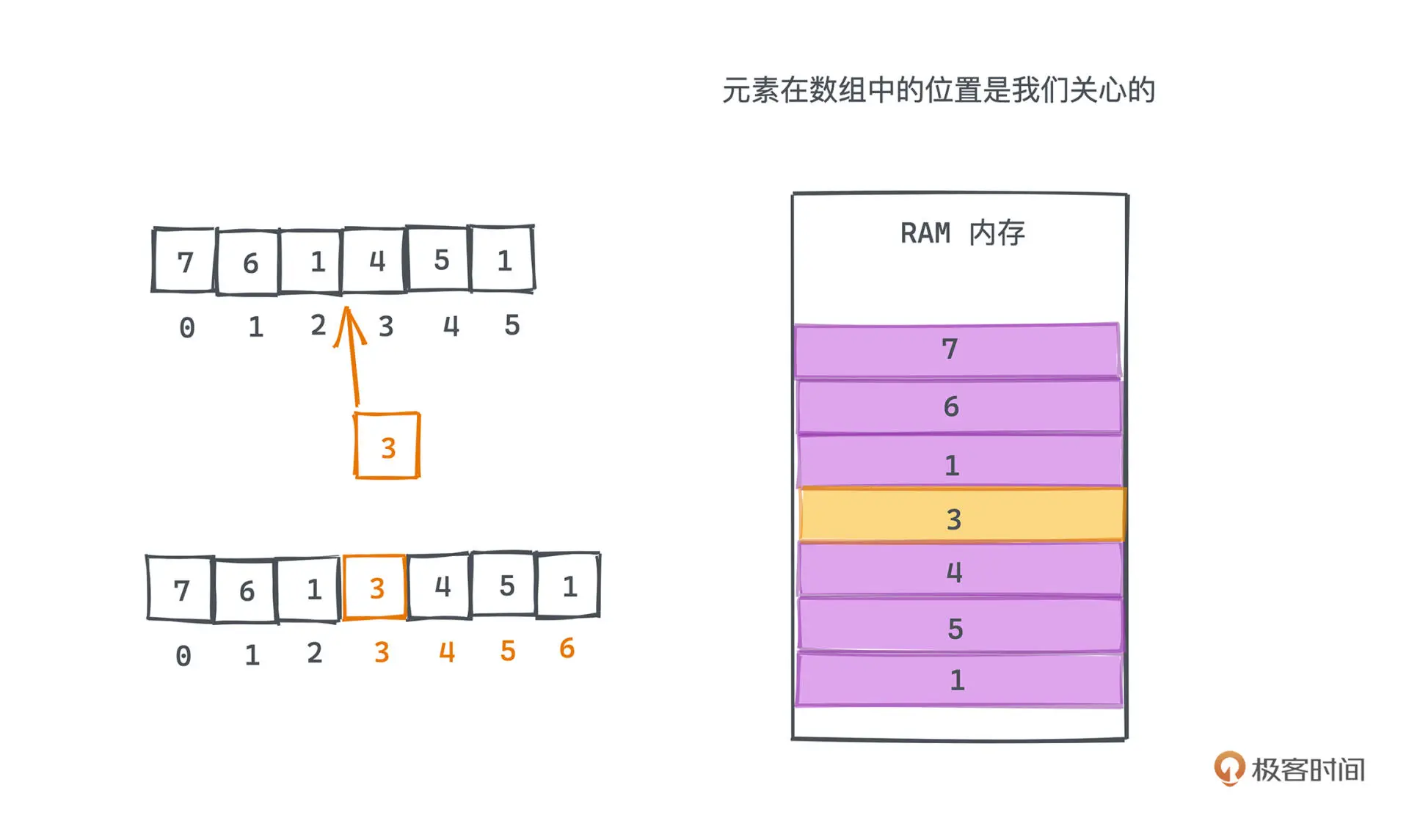
静态数组的元素个数是事先确定的
动态数组
动态数组将扩容的逻辑分装起来,方便用户使用
Vector 源码分析
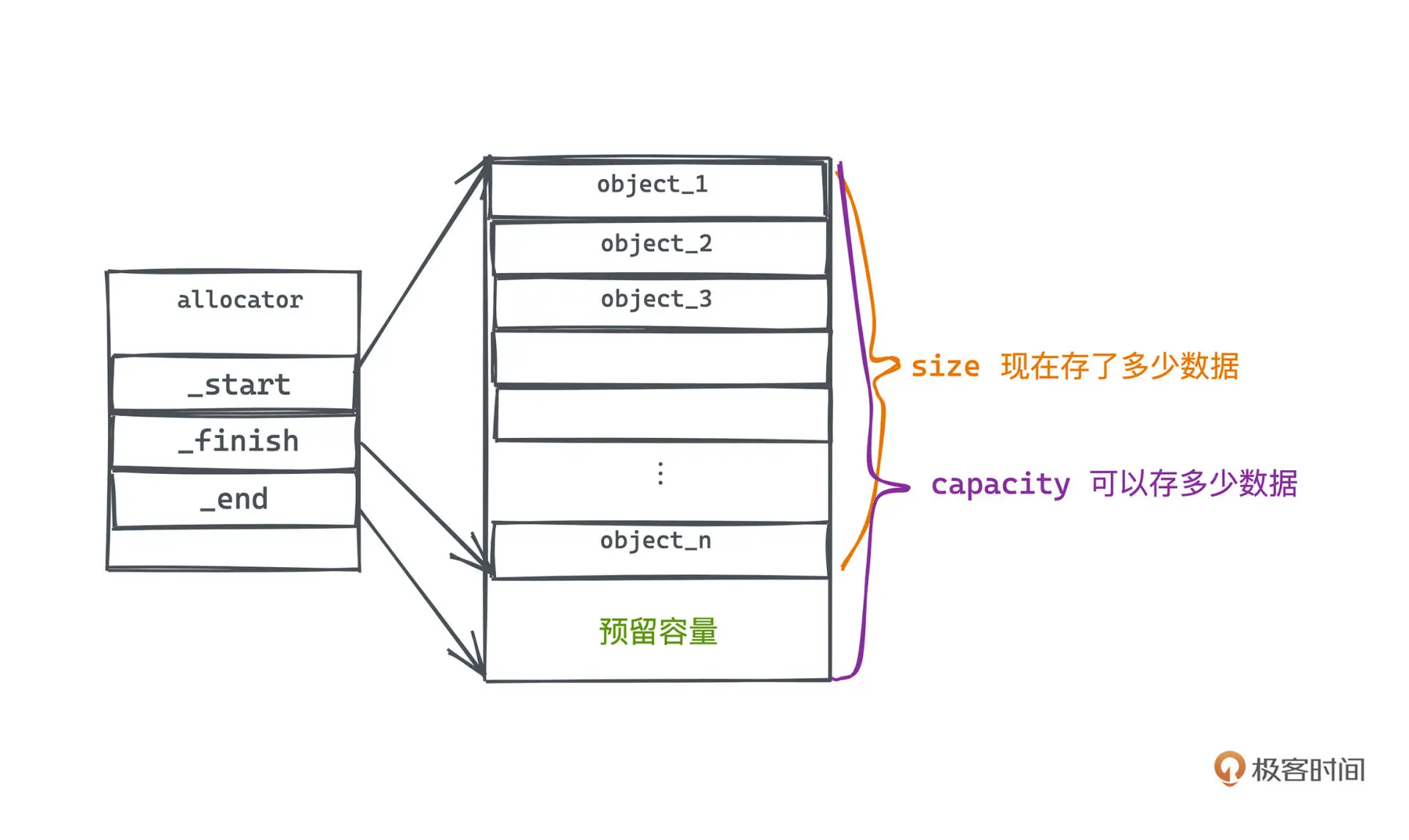
vector 中有三个关键指针
- _start: 指向 vector 第一个元素
- _finish: 指向 vector 最后一个元素
- _end: 指向 vector 预留容量的边界
1
2
3
4
5
6
7
8
9
10
|
template <class _Tp, class _Alloc = __STL_DEFAULT_ALLOCATOR(_Tp) >
class vector : protected _Vector_base<_Tp, _Alloc>
{
...
protected:
_Tp* _M_start; //表示目前使用空间的头
_Tp* _M_finish; //表示目前使用空间的尾
_Tp* _M_end_of_storage; //表示目前可用空间的尾
...
};
|
扩容实现源码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
|
void push_back(const _Tp& __x) {//在最尾端插入元素
if (_M_finish != _M_end_of_storage) {//若有可用的内存空间
construct(_M_finish, __x);//构造对象
++_M_finish;
}
else//若没有可用的内存空间,调用以下函数,把x插入到指定位置
_M_insert_aux(end(), __x);
}
template <class _Tp, class _Alloc>
void
vector<_Tp, _Alloc>::_M_insert_aux(iterator __position, const _Tp& __x)
{
if (_M_finish != _M_end_of_storage) {
construct(_M_finish, *(_M_finish - 1));
++_M_finish;
_Tp __x_copy = __x;
copy_backward(__position, _M_finish - 2, _M_finish - 1);
*__position = __x_copy;
}
else {
const size_type __old_size = size();
const size_type __len = __old_size != 0 ? 2 * __old_size : 1;
iterator __new_start = _M_allocate(__len);
iterator __new_finish = __new_start;
__STL_TRY {
__new_finish = uninitialized_copy(_M_start, __position, __new_start);
construct(__new_finish, __x);
++__new_finish;
__new_finish = uninitialized_copy(__position, _M_finish, __new_finish);
}
__STL_UNWIND((destroy(__new_start,__new_finish),
_M_deallocate(__new_start,__len)));
destroy(begin(), end());
_M_deallocate(_M_start, _M_end_of_storage - _M_start);
_M_start = __new_start;
_M_finish = __new_finish;
_M_end_of_storage = __new_start + __len;
}
}
|
- 22-25 行,主要做的事情就是读取原有的 vector 大小 old_size,再从内存里申请一段新的空间,大小为 2*old_size,创建新的首尾指针并指向新的空间。
- 26-31 行,将老空间里的数据逐一搬到新的空间里,并在最后添加新的元素。这样就完成了扩容的主要目的,这是一个 O(n) 复杂度的操作,因为你需要对原数组进行逐一的深拷贝。
- 最后,在 32-38 行,我们需要做一些清理和收尾工作,释放掉老的数组空间和指针,将容器的首尾及容量指针都更新到对应的位置。
假设插入 N 次, 那么总拷贝次数就是 1 加到 2 x 次方, x 是 logn x向上取整
1
|
1 + 2 + 4 + 8 + … + 2 ** x = 2 ** (x+1) − 1
|
这样插入 N 次的复杂度为 O(N), 平均每次插入操作复杂度为 O(1).
第二讲 双向链表 list
链表简介
链表同样是一种序列式结构,但无需连续内存,使用通过指针相连的节点来存储。
每个节点分为两个部分,一个是数据域 data field,另外一个是 引用域 reference field。
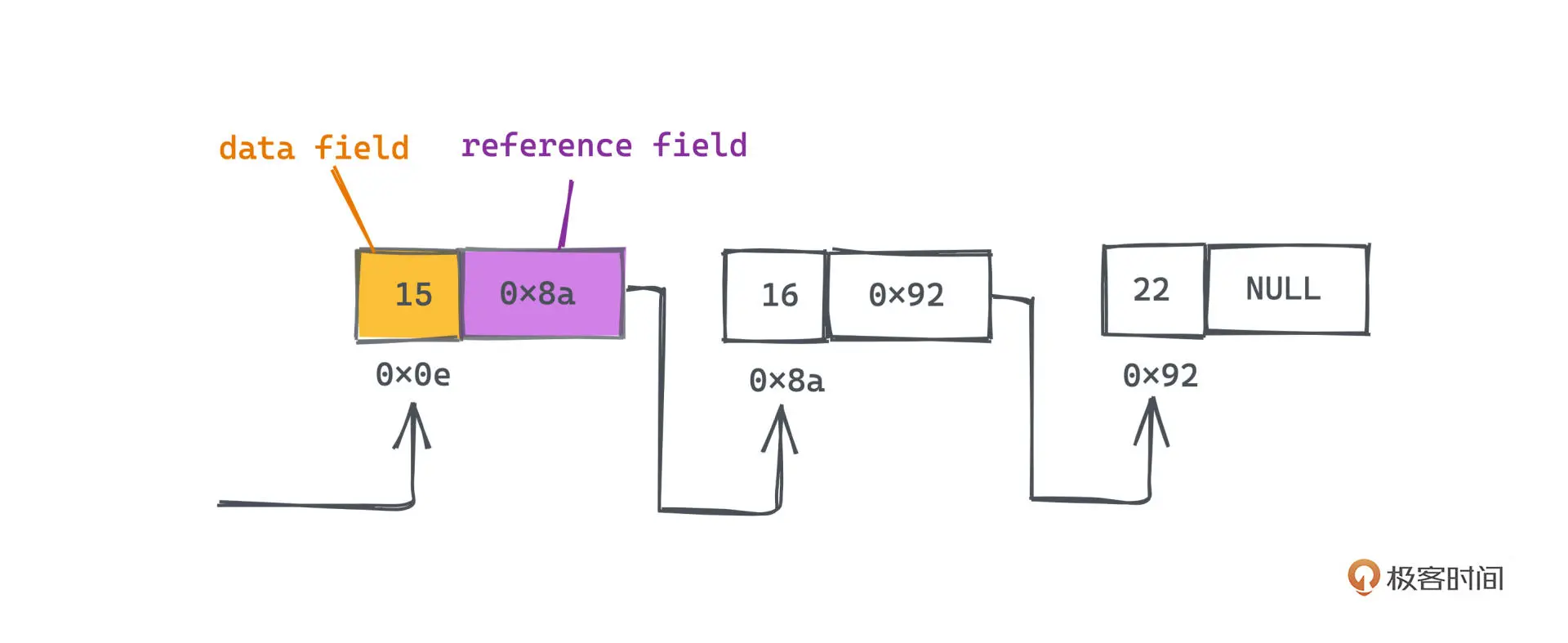
因为通过 指针串联 ,所以在任何位置插入或者删除节点,只需要 O(1) 的复杂度。
链表种类
链表通常有三种形式:单向链表、双向链表、循环链表
STL list 实现
list 是 STL 中的链表容器,实现了双向循环链表
节点实现
1
2
3
4
5
6
|
template <class T>
struct __list_node {
__list_node<T>* next; // 前驱节点指针
__list_node<T>* prev; // 后继节点指针
T data; //存储数据
};
|
迭代器实现
迭代器提供用于遍历的最重要的接口,支持的操作就是自增和增减
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
template<typename T>
struct __list_iterator{
typedef __list_iterator<T> self;
typedef __list_node<T>* link_type;
link_type ptr; //成员
__list_iterator(link_type p = nullptr):ptr(p){}
}
T& operator *(){return ptr->data;}
T* operator ->(){return &(operator*());}
// 类似 ++x 返回next节点
self& operator++(){
ptr = ptr->next;
return *this;
}
// 类似 x++ 返回当前节点
self operator++(int){
self tmp = *this;
++*this;
return tmp;
}
// 类似 --x 返回prev节点
self& operator--(){
ptr = ptr->prev;
return *this;
}
// 类似 x-- 返回当前节点
self operator--(int){
self tmp = *this;
--*this;
return tmp;
}
bool operator==(const __list_iterator& rhs){
return ptr == rhs.ptr;
}
bool operator!=(const __list_iterator& rhs){
return !(*this==rhs);
}
|
数据结构实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
template<typename T>
class list{
protected:
typedef __list_node<T> list_node; // 显示定义list_node类型
typedef allocator<list_node> nodeAllocator; // 定义allocator类型
public:
typedef T value_type;
typedef T& reference;
typedef value_type* pointer;
typedef list_node* link_type;
typedef const value_type* const_pointer;
typedef size_t size_type;
public:
typedef __list_iterator<value_type> iterator; // 迭代器类型重写
private:
link_type node; // 只要一个指针,便可表示整个环状双向链表
// ......
}
|
每个链表,都会有一个虚拟节点,用于标记整个循环链表的首尾连接处,它是链表的开始,也是链表的结尾,
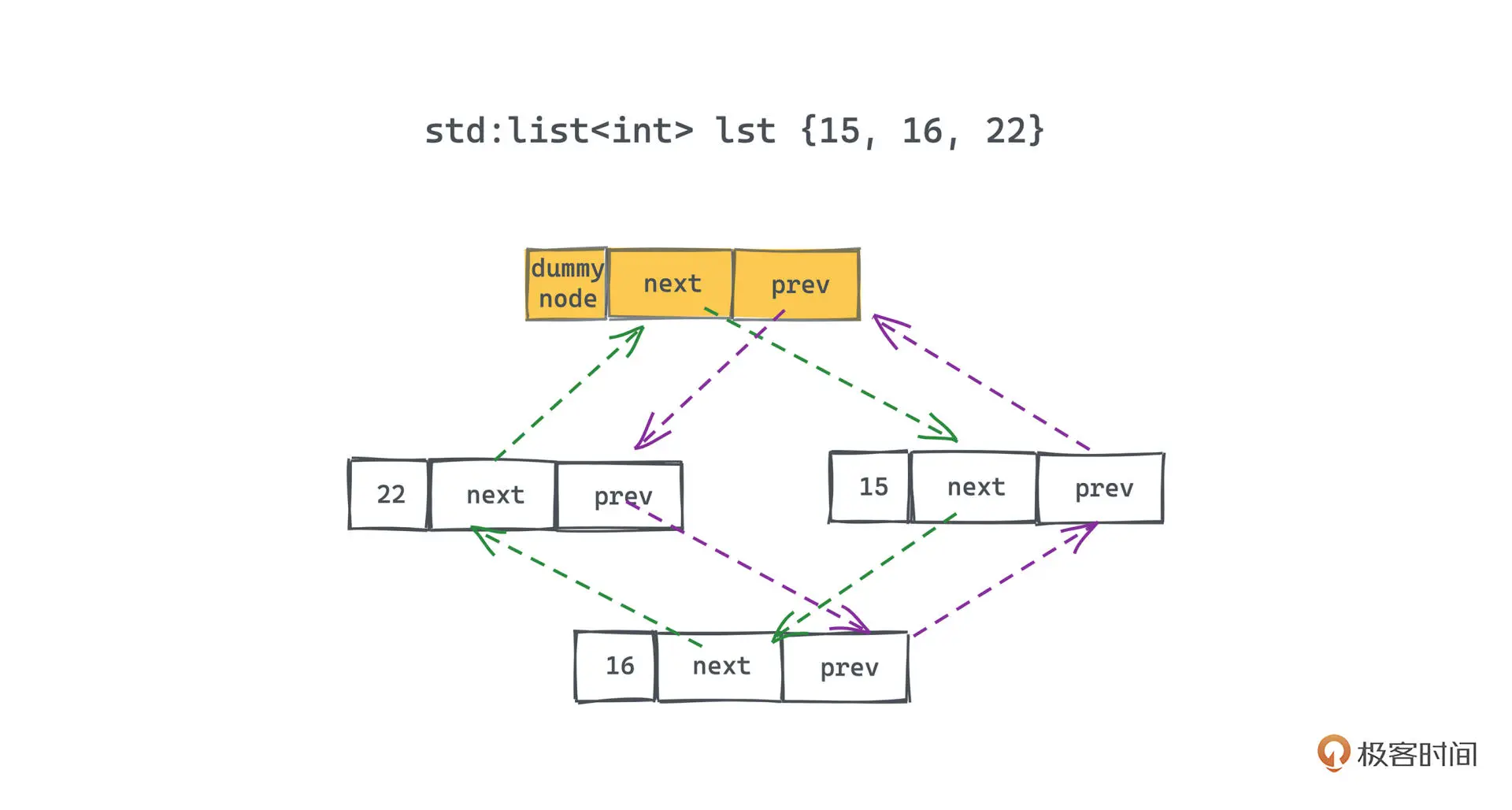
迭代示例代码:
1
2
|
for (std::list<int>::iterator it=mylist.begin(); it!= mylist.end();++it)
std::cout << ' ' << *it;
|
基本操作实现
初始化
1
2
3
4
5
6
7
|
void empty_initialize() {
node = get_node(0);
node->next = node; // next 指针指向自身
node->prev = node; // prev 指针指向自身
}
link_type get_node() { return list_node_allocator:allocate(); }
|
插入
1
2
3
4
5
6
7
8
|
iterator insert(iterator position, const T& x) {
lik_type tmp = create_node(x); // 创建一个临时节点
tmp->next = position.node; // 将该节点的后继指针指向当前位置的节点
tmp->prev = position.node->prev; // 将该节点的前驱指针指向当前位置的前驱节点
(link_type(position.node->prev))->next = tmp; // 将前驱节点本来指向当前节点的后继指针改为指向该临时节点
position.node->prev = tmp; // 同样,当前位置的前驱指针也要修改为指向该临时节点
return tmp;
}
|
删除
1
2
3
4
5
6
7
8
|
iterator erase(iterator position) {
link_type next_node = link_type(position.node->next);
link_type prev_node = link_type(position.node->prev);
prev_node->next = next_node;
next_node->prev = prev_node;
destroy_node(position.node);
return iterator(next_node);
}
|
push / pop
1
2
3
4
5
6
7
|
void pop_front() { erase(begin()) };
void pop_back() {
iterator tmp = end();
erase(--tmp);
}
push_back(const T& x) { insert(end(), x); }
|
第三讲 双端队列
队列
队列是一种先进先出的序列式数据结构
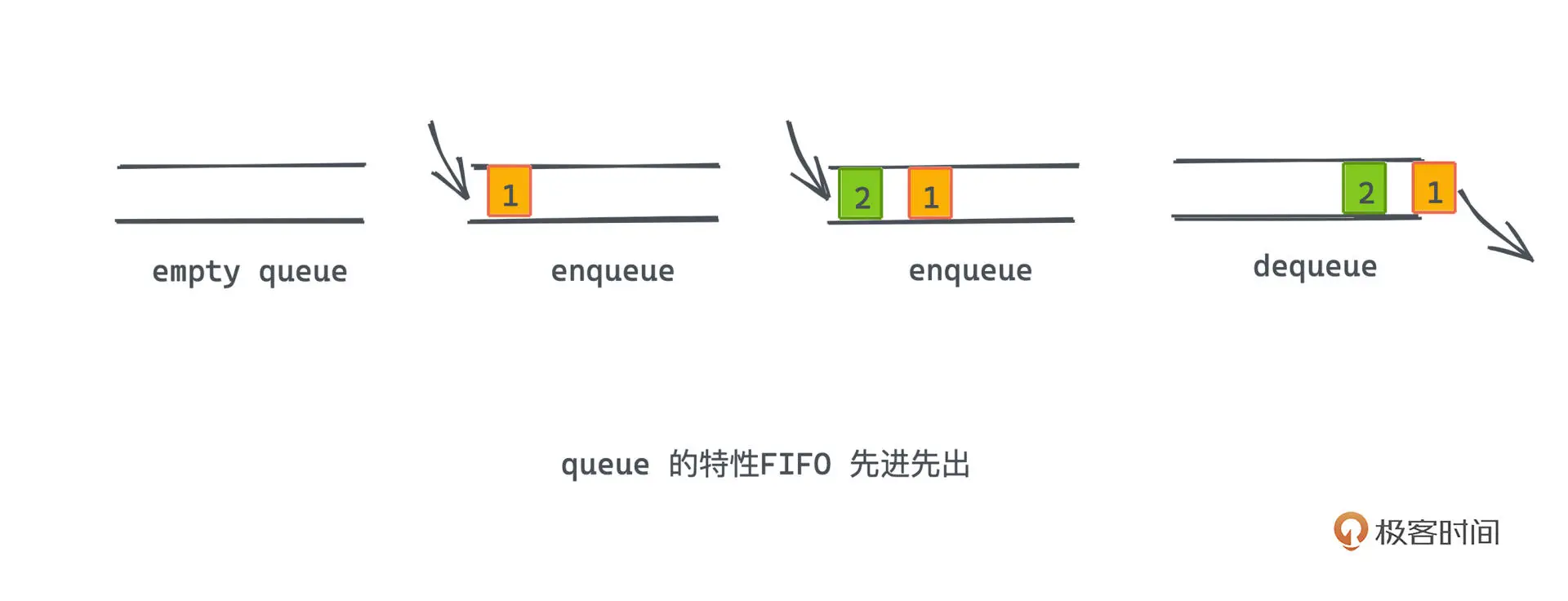
双端队列
双端队列可以在队列的两端都可以进行出队和入队操作
Deque 实现
内存布局
deque 的内存布局是由一段段连续的空间,
用另一个类似数组的东西将这些空间的地址信息拼接在一起组成的。
在首尾插入和删除数据的复杂度都是 O(1)
deque 既不像 vector 那样每次扩容都需要付出复制和拷贝的高昂代价,
也不会像 list 那样每次插入一个新节点都需要申请一次内存。
deque 使用 map 变量来管理真正用于存储队列元素的一段段连续线性空间
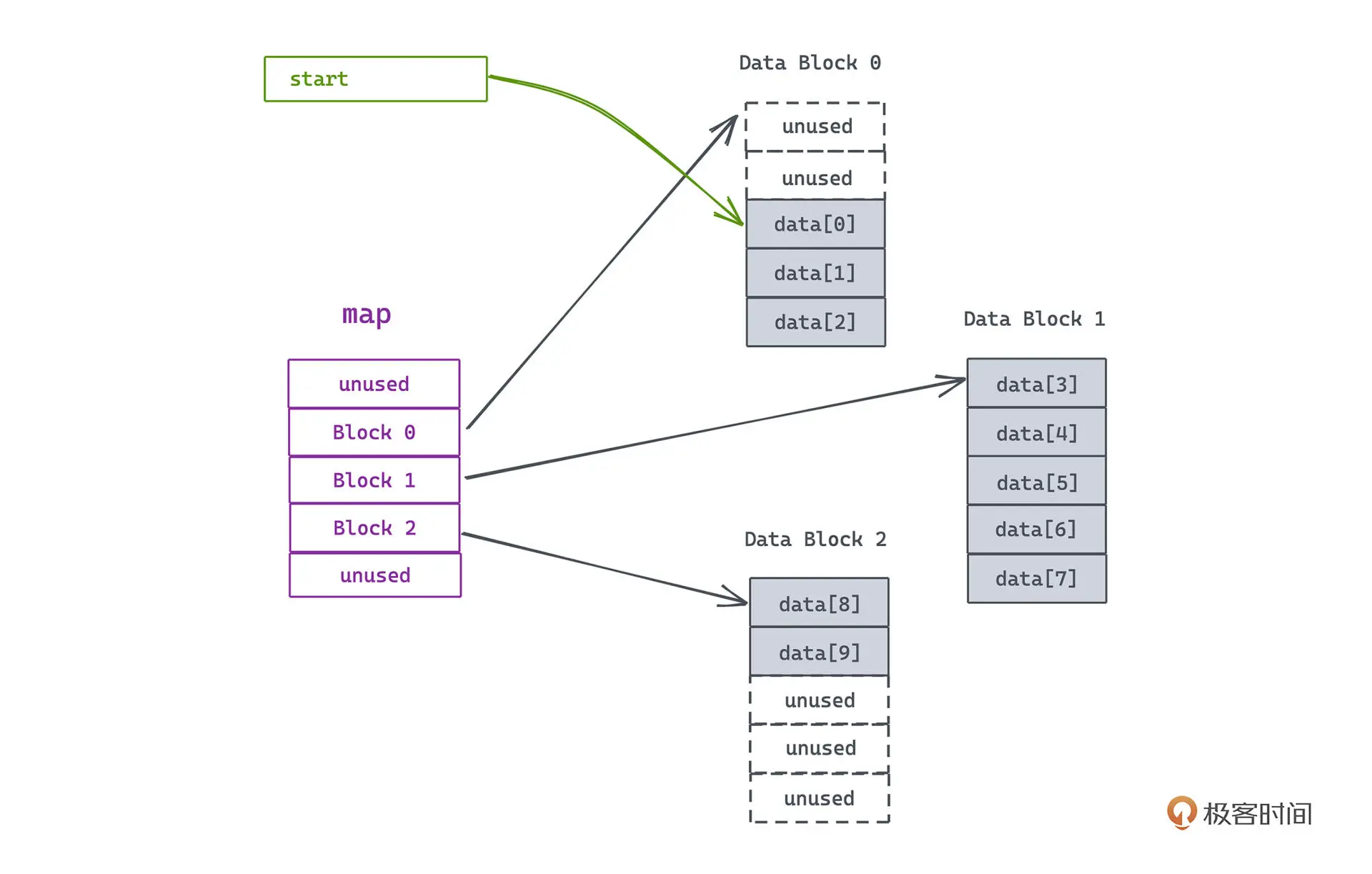
可以认为 map 是一个数组,每个元素指向了一段缓冲区地址,而缓冲区对应了一段指定大小的连续内存空间,默认大小为 512 bytes
1
2
3
4
5
6
7
8
9
10
|
template <class _Tp, class _Alloc>
class _Deque_base {
...
protected:
_Tp** _M_map;
size_t _M_map_size;
iterator _M_start;
iterator _M_finish;
...
}
|
迭代器
因为 deque 底层实质是分段连续空间,迭代器需要找到相邻的缓冲区以及当前所处位置
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
|
template <class _Tp, class _Ref, class _Ptr>
struct _Deque_iterator {
typedef _Deque_iterator<_Tp, _Tp&, _Tp*> iterator;
typedef _Deque_iterator<_Tp, const _Tp&, const _Tp*> const_iterator;
static size_t _S_buffer_size() { return __deque_buf_size(sizeof(_Tp)); }
...
typedef _Tp** _Map_pointer; // 缓冲区指针
...
_Tp* _M_cur; // 当前缓冲区的位置
_Tp* _M_first; // 缓冲区的左边界线
_Tp* _M_last; // 缓冲区的右边界
_Map_pointer _M_node;
_Deque_iterator(_Tp* __x, _Map_pointer __y)
: _M_cur(__x), _M_first(*__y),
_M_last(*__y + _S_buffer_size()), _M_node(__y) {}
}
_Self& operator++() {
++_M_cur;
if (_M_cur == _M_last) {
_M_set_node(_M_node + 1);
_M_cur = _M_first;
}
return *this;
}
void _M_set_node(_Map_pointer __new_node) {
_M_node = __new_node;
_M_first = *__new_node;
_M_last = _M_first + difference_type(_S_buffer_size());
}
_Self& operator--() {
if (_M_cur == _M_first) {
_M_set_node(_M_node - 1);
_M_cur = _M_last;
}
--_M_cur;
return *this;
}
|
基础操作
push 操作
- 如果当前缓冲区有空间,直接插入
- 如果 map 有空间,则新建一个缓冲区存入map
- 如果 map 空间不足,则分为两种情况
- map 使用率过半,就申请更大的空间,将老的 map 数据拷贝到新区域,map 指向的缓冲区不变
- map 使用率小于一半,将数据重新调整到 map 中间的位置
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
void push_back(const value_type& __t) {
if (_M_finish._M_cur != _M_finish._M_last - 1) {
construct(_M_finish._M_cur, __t);
++_M_finish._M_cur;
}
else
_M_push_back_aux(__t);
}
template <class _Tp, class _Alloc>
void deque<_Tp,_Alloc>::_M_push_back_aux()
{
_M_reserve_map_at_back();
*(_M_finish._M_node + 1) = _M_allocate_node();
__STL_TRY {
construct(_M_finish._M_cur);
_M_finish._M_set_node(_M_finish._M_node + 1);
_M_finish._M_cur = _M_finish._M_first;
}
__STL_UNWIND(_M_deallocate_node(*(_M_finish._M_node + 1)));
}
|
pop 操作
如果迭代器和缓冲区的首位置相同,则除了释放当前的内存,还需要释放掉整段缓冲区的内存。
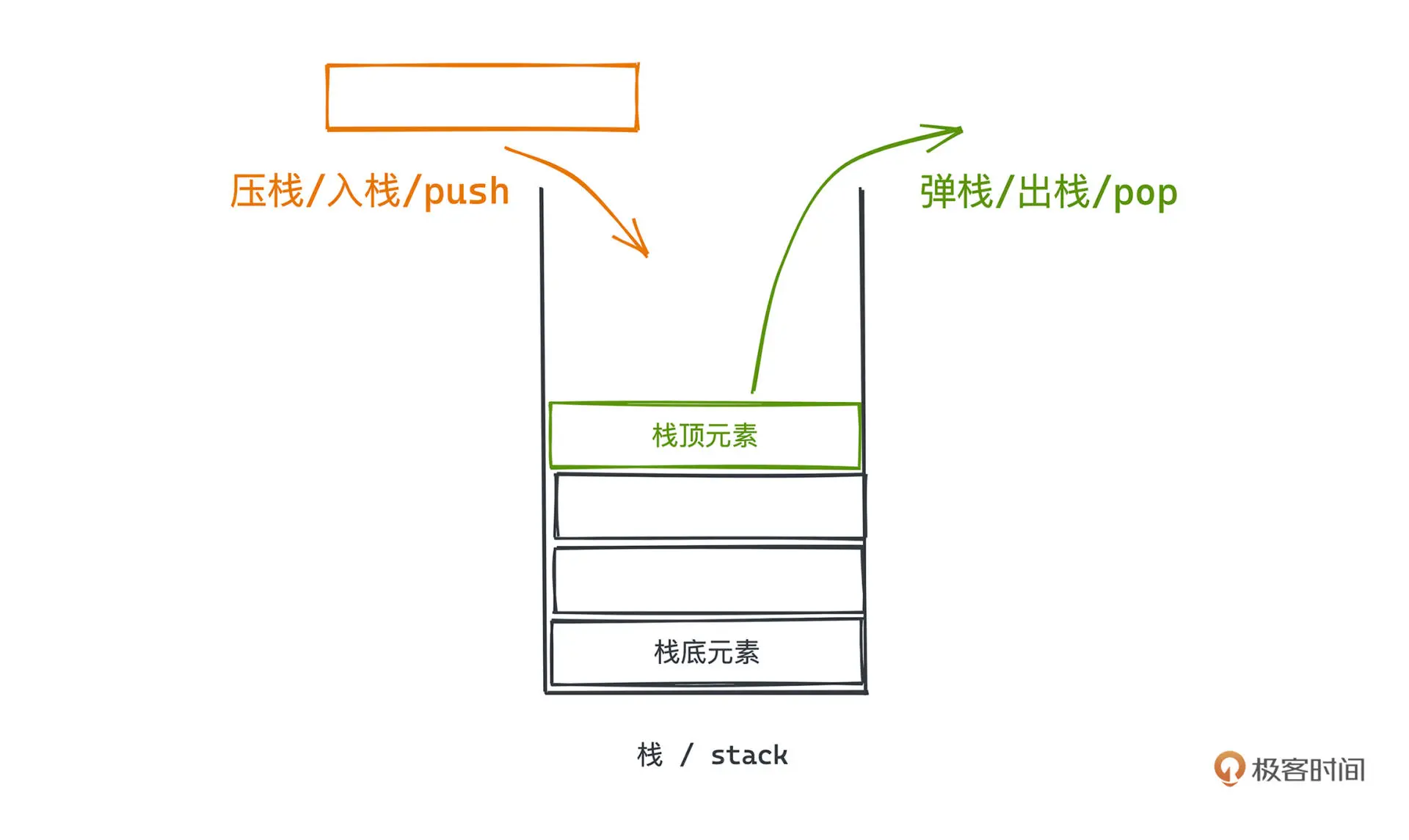
第四讲 栈
栈区是有结构和固定大小的,区块按照次序存放,每个线程独占一个栈区,总大小也是事先确定的。
特性: LIFO
栈只能从栈顶删除或者插入元素,所以保证了后进先出的特性
STL 实现
STL 中使用了 deque 来实现 stack ,这种封装模式称为适配器模式,stack 也被看做是一种
container adapter
数据结构定义
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
template<typename _Tp, typename _Sequence = deque<_Tp> >
class stack
{
public:
typedef typename _Sequence::value_type value_type;
typedef typename _Sequence::reference reference;
typedef typename _Sequence::const_reference const_reference;
typedef typename _Sequence::size_type size_type;
typedef _Sequence container_type;
protected:
_Sequence c; // stack 底层容器; 默认为 deque
public:
reference
top()
{
__glibcxx_requires_nonempty();
return c.back();
}
void push(const value_type& __x) { c.push_back(__x); }
void pop() {c.pop_back();}
...
}
|
第五讲 HashMap
散列
散列函数的本质是将一个更大且可能不连续空间,映射到一个空间有限的数组里,
从而借用数组基于下标 O(1) 快速随机访问数组元素的能力。
但设置一个合理的散列函数是个非常有挑战的事情,比如 26 进制的散列函数就有一个巨大的缺陷,
就是它所需的数组空间太大了,三位长度的元素就需要开一个接近 20000 (26^3)大小的计数数组。
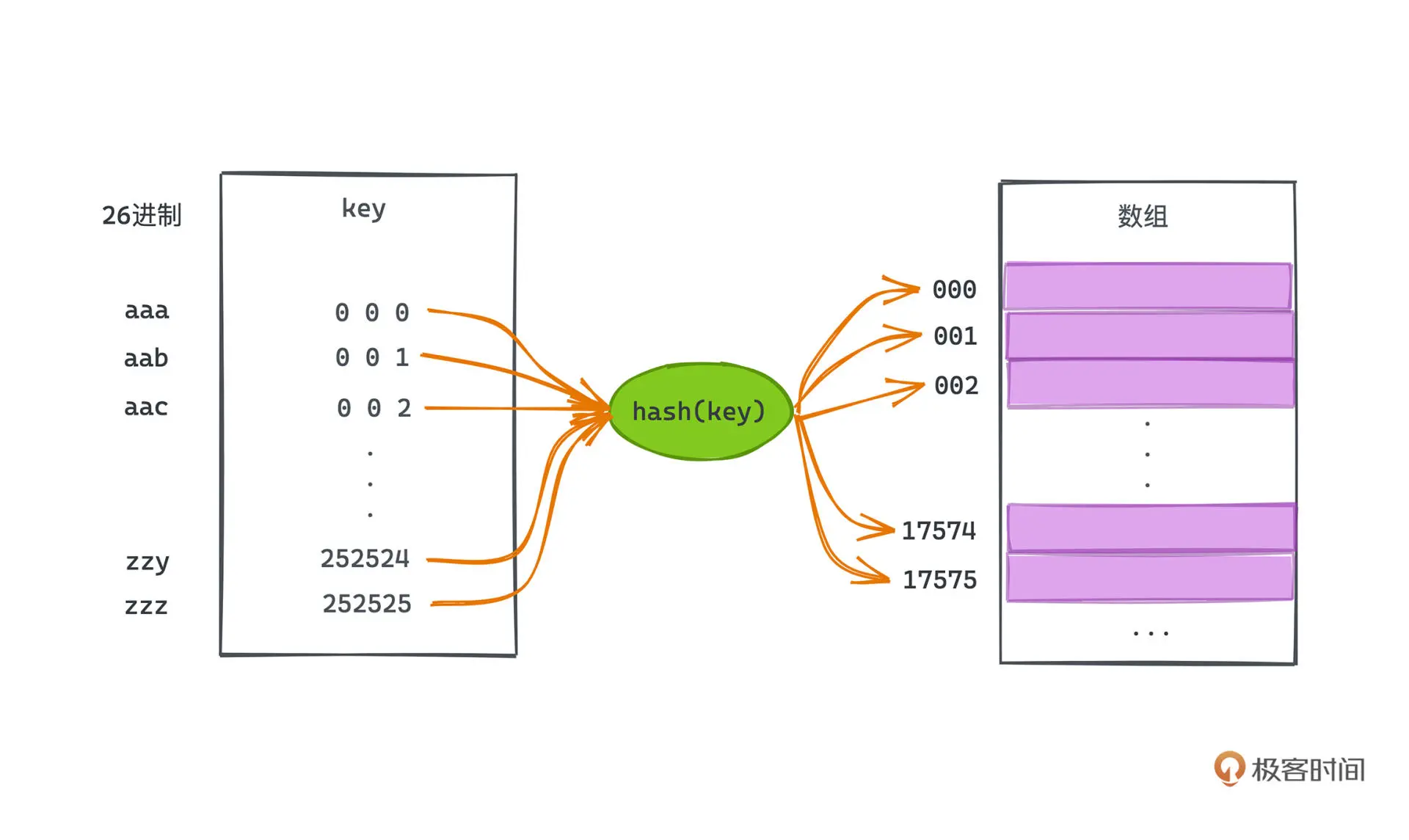
这时我们需要对哈希值进行 取模运算,但取模之后会遇到一个新问题:哈希碰撞。
JDK 实现
hash 方法
1
2
3
4
|
static final int hash(Object key) {
int h;
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
|
String 类型的 hashCode 方法
1
2
3
4
5
6
7
8
9
10
11
12
13
|
public int hashCode() {
int h = hash;
if (h == 0 && !hashIsZero) {
h = isLatin1() ? StringLatin1.hashCode(value)
: StringUTF16.hashCode(value);
if (h == 0) {
hashIsZero = true;
} else {
hash = h;
}
}
return h;
}
|
StringUTF16 hashCode 实现
1
2
3
4
5
6
7
8
9
10
|
public static int hashCode(byte[] value) {
int h = 0;
int length = value.length >> 1;
for (int i = 0; i < length; i++) {
h = 31 * h + getChar(value, i);
}
return h;
}
// like s[0]*31^(n-1) + s[1]*31^(n-2) + ... + s[n-1]
|
在哈希计算时倾向于用奇素数进行乘法运算,因为使用偶数时相当于进行移位运算,部分位的信息丢失可能增加哈希冲突概率。
使用 31 是因为 31 * i 编译器可以自动转换成 (i « 5) - i
^ h »> 16
^ h >>> 16 把 高 16位的 信息叠加到低16位,这样在取模的时候就可以用到高位信息,
减少冲突概率。
table 实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
|
transient Node<K,V>[] table;
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
boolean evict) {
Node<K,V>[] tab; Node<K,V> p; int n, i;
//在tab尚未初始化、或者对应槽位链表未初始化时,进行相应的初始化操作
if ((tab = table) == null || (n = tab.length) == 0)
n = (tab = resize()).length;
if ((p = tab[i = (n - 1) & hash]) == null)
tab[i] = newNode(hash, key, value, null);
else {
Node<K,V> e; K k;
// 查找 key 对应的节点
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
e = p;
else if (p instanceof TreeNode)
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
else {
// 遍历所有节点 依次查找
for (int binCount = 0; ; ++binCount) {
if ((e = p.next) == null) {
p.next = newNode(hash, key, value, null);
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
treeifyBin(tab, hash); // 链表转化成红黑树
break;
}
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
break;
p = e;
}
}
if (e != null) { // existing mapping for key
V oldValue = e.value;
if (!onlyIfAbsent || oldValue == null)
e.value = value;
afterNodeAccess(e);
return oldValue;
}
}
++modCount;
if (++size > threshold)
resize();
afterNodeInsertion(evict);
return null;
}
|
table 是经过散列之后映射到的内部连续数组,通过 hash 函数的计算,我们可以
基于数组的下标快速访问到 key 对应的元素, 元素存储的是 Node 类型。
Node 的具体实现可以是链表或者红黑树,当链表足够长时,会将链表转化成红黑树。
当table 中元素数量达到阈值时,会触发扩容逻辑
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
|
final Node<K,V>[] resize() {
Node<K,V>[] oldTab = table;
int oldCap = (oldTab == null) ? 0 : oldTab.length;
int oldThr = threshold;
int newCap, newThr = 0;
if (oldCap > 0) {
if (oldCap >= MAXIMUM_CAPACITY) {
threshold = Integer.MAX_VALUE;
return oldTab;
}
else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
oldCap >= DEFAULT_INITIAL_CAPACITY)
newThr = oldThr << 1; // 翻倍扩容
}
else if (oldThr > 0) // 初始化的时候 capacity 设置为初始化阈值
newCap = oldThr;
else { // 没有初始化 采用默认值
newCap = DEFAULT_INITIAL_CAPACITY;
newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
}
if (newThr == 0) {
float ft = (float)newCap * loadFactor; // 用容量乘负载因子表示扩容阈值
newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
(int)ft : Integer.MAX_VALUE);
}
threshold = newThr;
@SuppressWarnings({"rawtypes","unchecked"})
Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
table = newTab;
if (oldTab != null) {
for (int j = 0; j < oldCap; ++j) {
Node<K,V> e;
if ((e = oldTab[j]) != null) {
oldTab[j] = null;
if (e.next == null)
newTab[e.hash & (newCap - 1)] = e;
else if (e instanceof TreeNode)
((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
else {
// 新扩容部分,标识为hi,原来的部分标识为lo
// JDK 1.8 之后引入用于解决多线程死循环问题 可参考:https://stackoverflow.com/questions/35534906/java-hashmap-getobject-infinite-loop
Node<K,V> loHead = null, loTail = null;
Node<K,V> hiHead = null, hiTail = null;
Node<K,V> next;
// 整体操作就是将j所对应的链表拆成两个部分
// 分别放到 j 和 j + oldCap 的槽位
do {
next = e.next;
if ((e.hash & oldCap) == 0) {
if (loTail == null)
loHead = e;
else
loTail.next = e;
loTail = e;
}
else {
if (hiTail == null)
hiHead = e;
else
hiTail.next = e;
hiTail = e;
}
} while ((e = next) != null);
if (loTail != null) {
loTail.next = null;
newTab[j] = loHead;
}
if (hiTail != null) {
hiTail.next = null;
newTab[j + oldCap] = hiHead;
}
}
}
}
}
return newTab;
}
|
第六讲 红黑树
二分查找树
每个节点的左节点,要么为空,要么比当前节点小;右节点要么为空,要么比当前节点大。
当树的高度为 h 时,查找的时间复杂度为 O(h)
平衡二分查找树
在一些情况下,二分查找树可能会退化成链表
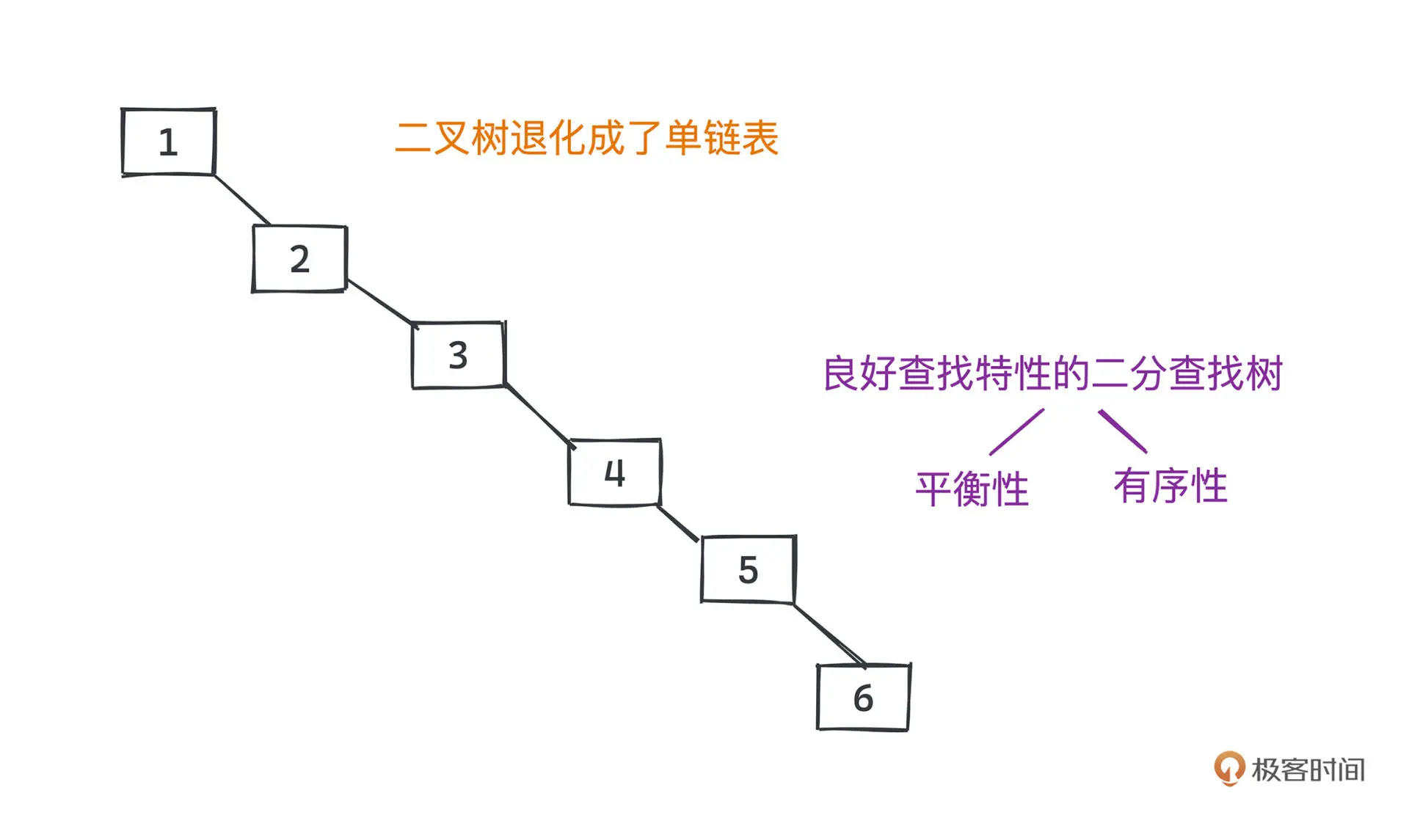
平衡二分查找树的叶子节点高度差不超过 1
2-3 树
2-3 树是一种平衡查找树的实现,除了普通的 2 节点外,引入了 3 节点,这为自平衡增加了很大的灵活性。
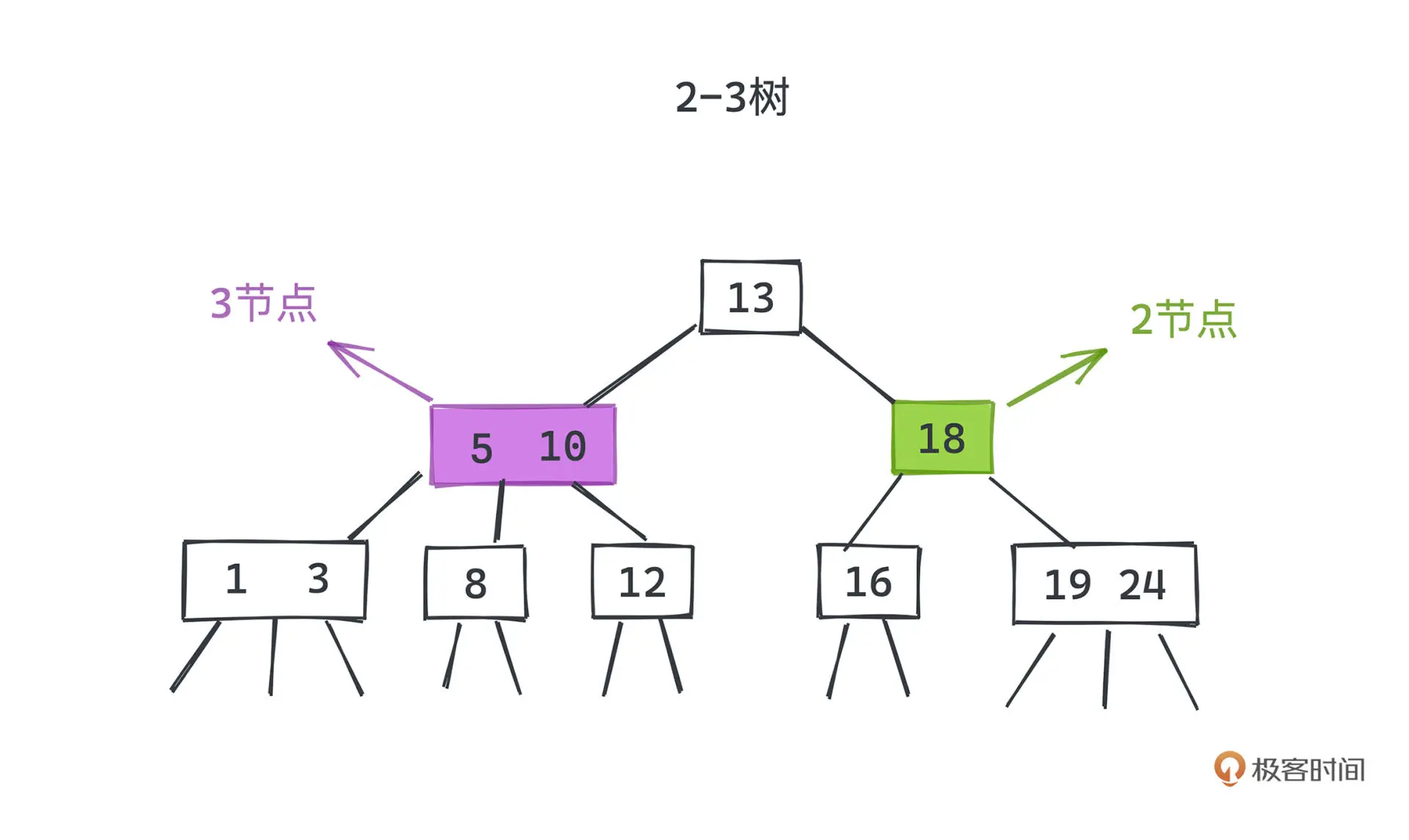
3 节点在 2 节点的基础上增加了一个键,构成了一个有两个键和三条链的结构
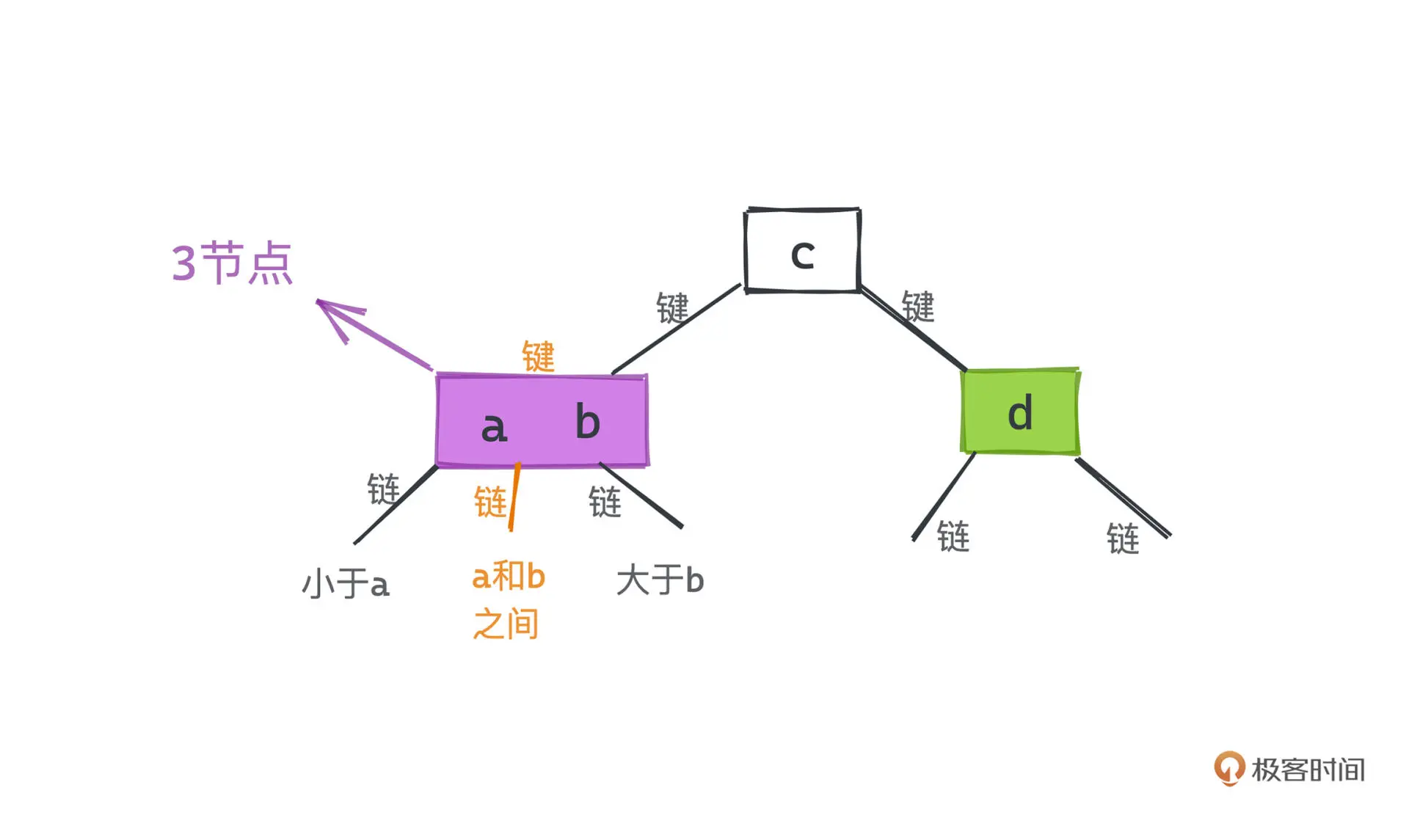
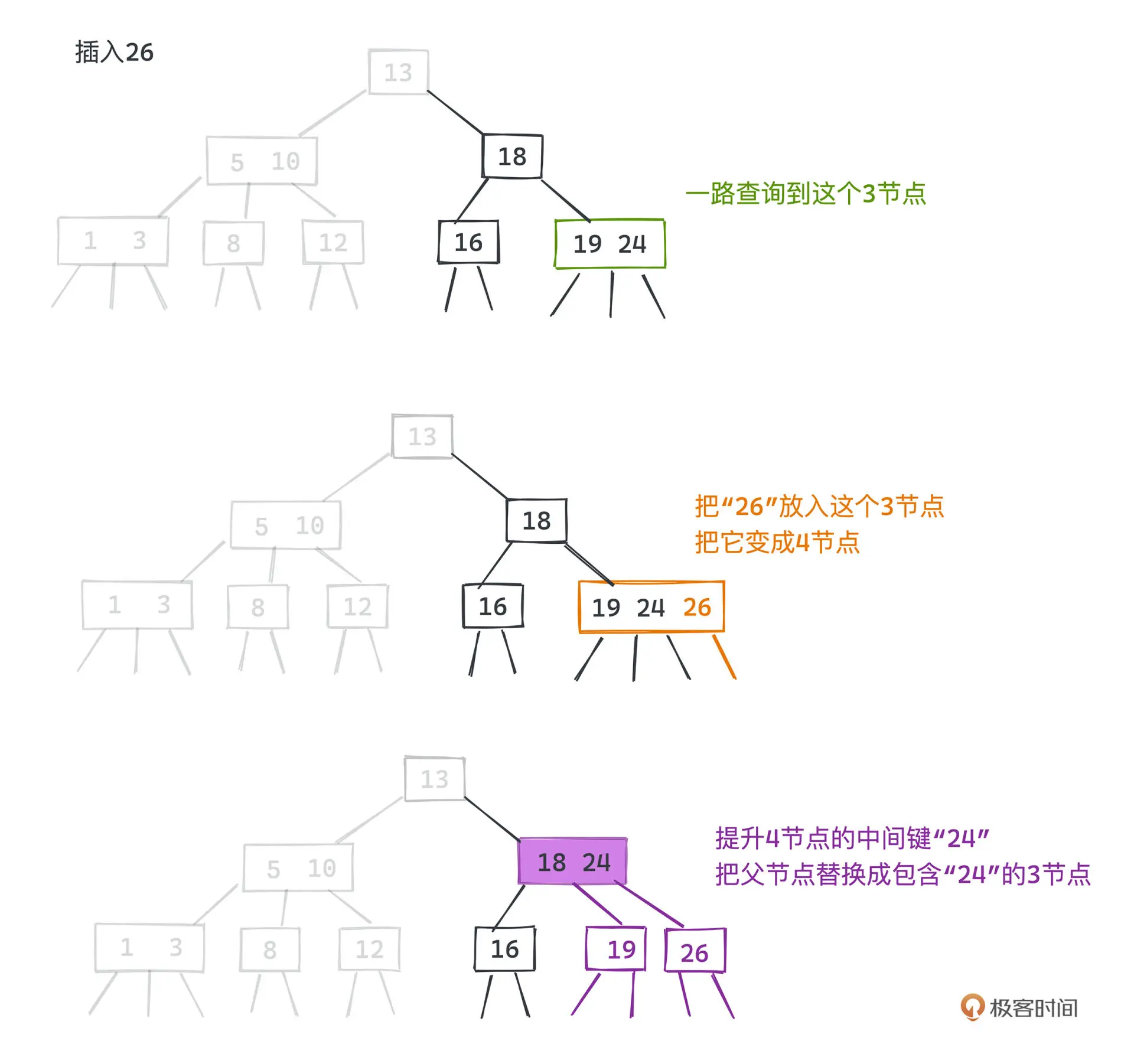
在插入过程中,如果遇到 2 节点,直接加个键将该节点升级为 3 节点就好。
遇到 3 节点时,首先将元素放入该节点,使之成为 4 节点,然后将四节点的中间键提升到上层,
红黑树
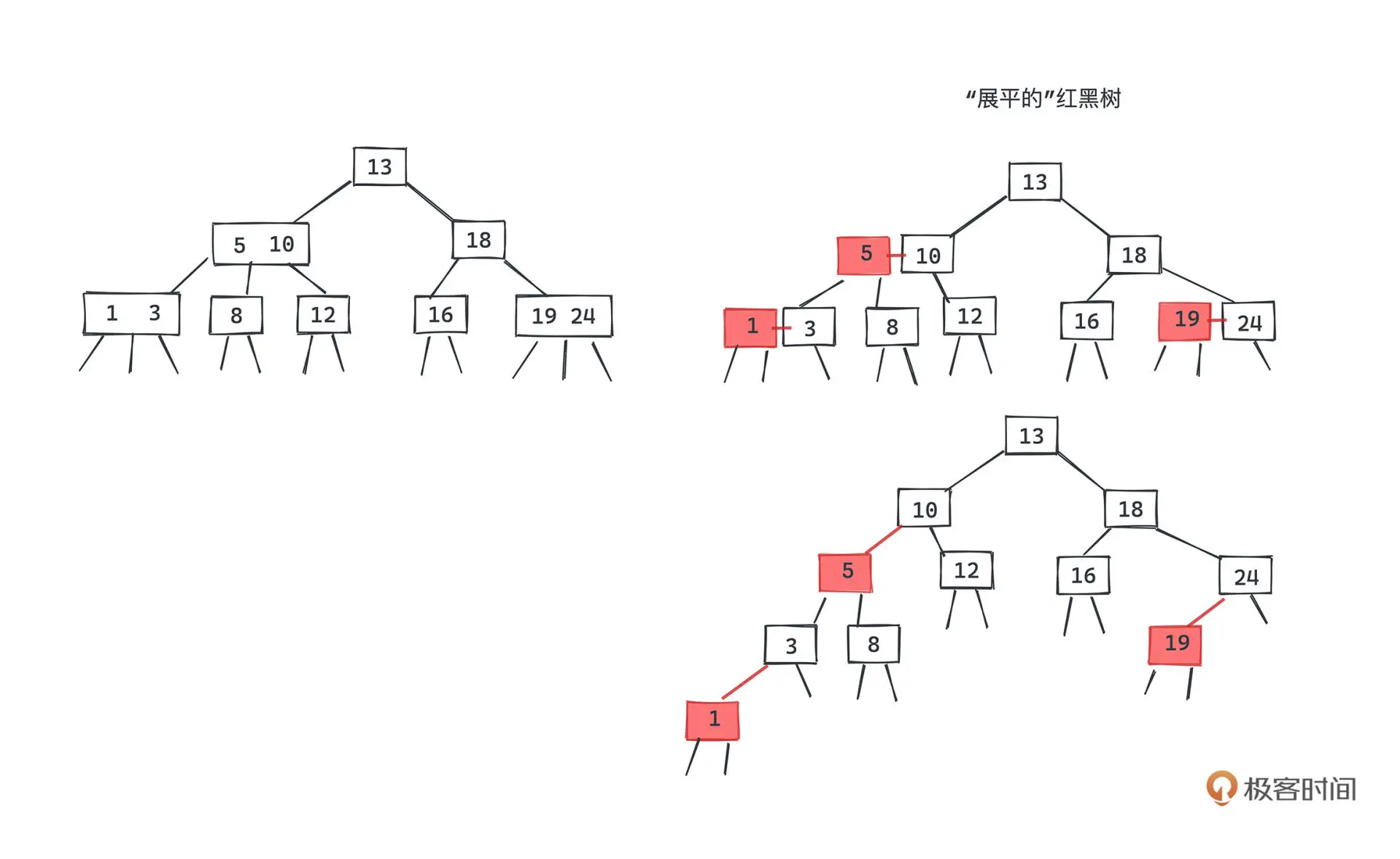
红黑树是采用标准的二叉查找树节点并附着颜色信息来表示 2-3 树的实现,每个
红色节点都和它的父节点一起构成了一个 3 节点。
红黑树有如下几个约束:
- 根节点为黑色
- 相邻节点不能同时为红色
- 每个节点到各个子节点的黑色节点数量相等
- 红节点只能作为左节点存在(这是左偏红黑树的要求)
一个 3 节点有两个键、三条链,那我们完全可以把一个以红节点为左子节点的黑节点和子节点一起看做一个 3 节点
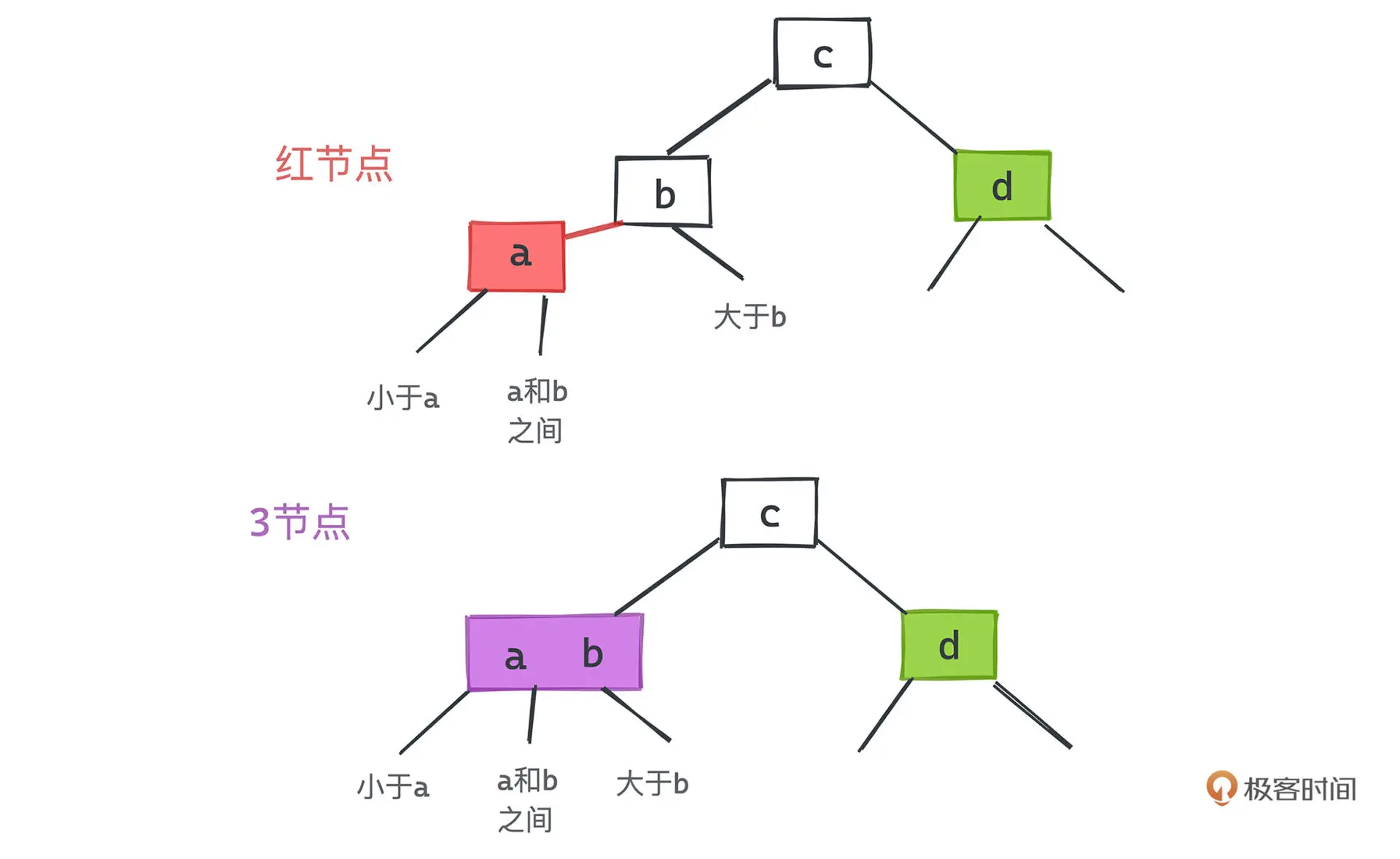
因为红节点只是 3 节点的一部分,那么对应到红黑树上,显然不会出现两个连续的红色节点。
2-3 树上,每个节点到叶子节点的数量一定是一样的,且每个节点只包含一个黑色节点,那么
红黑树到叶子节点路径中的黑色节点数量也必然是一样的。
旋转操作
旋转的作用在于处理插入和删除时产生的右偏红节点或者两个连续的红节点。
以左旋为例,本质就是将某个 3 节点从较小的键为根转移为较大的键为根
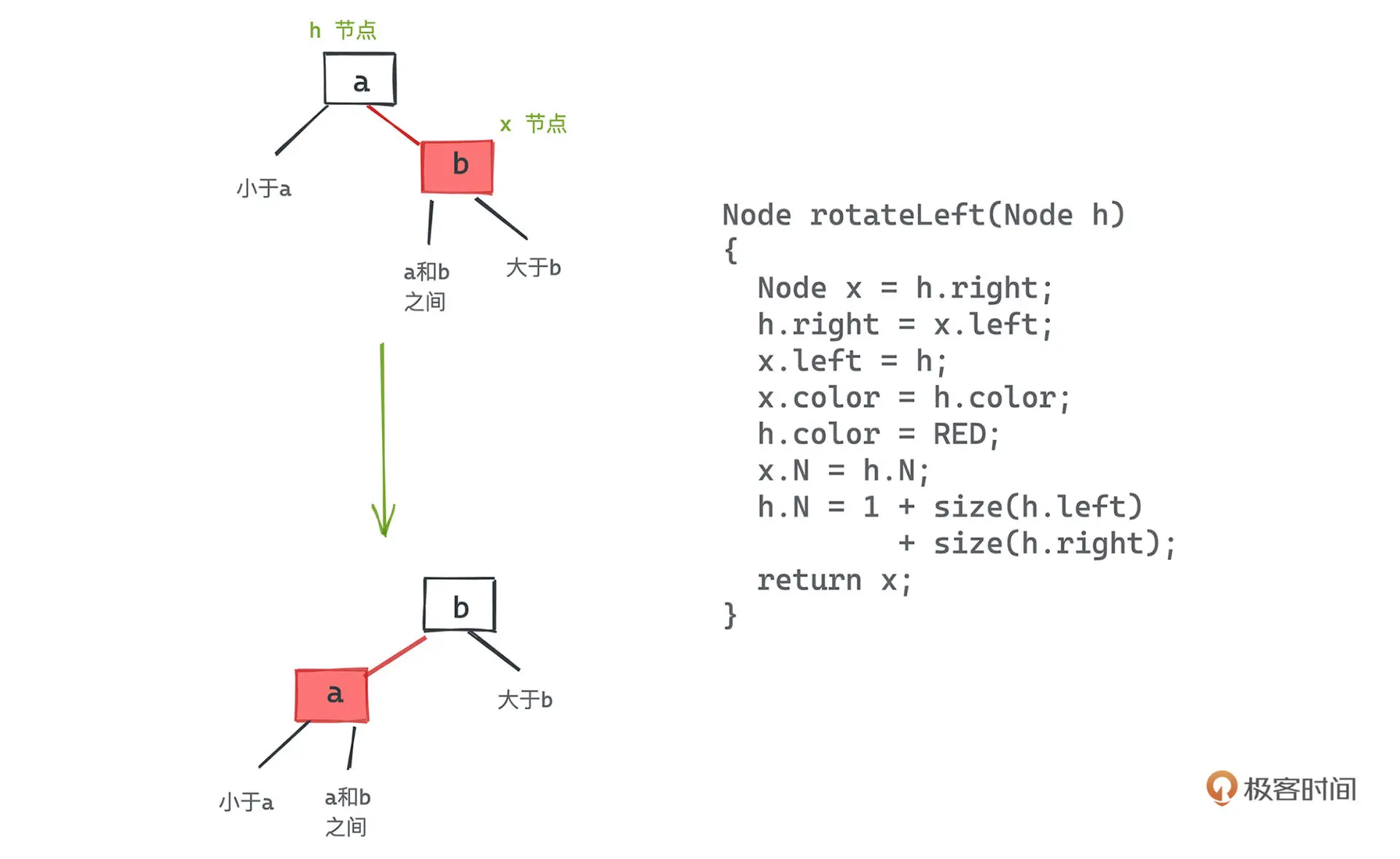
2 节点插入
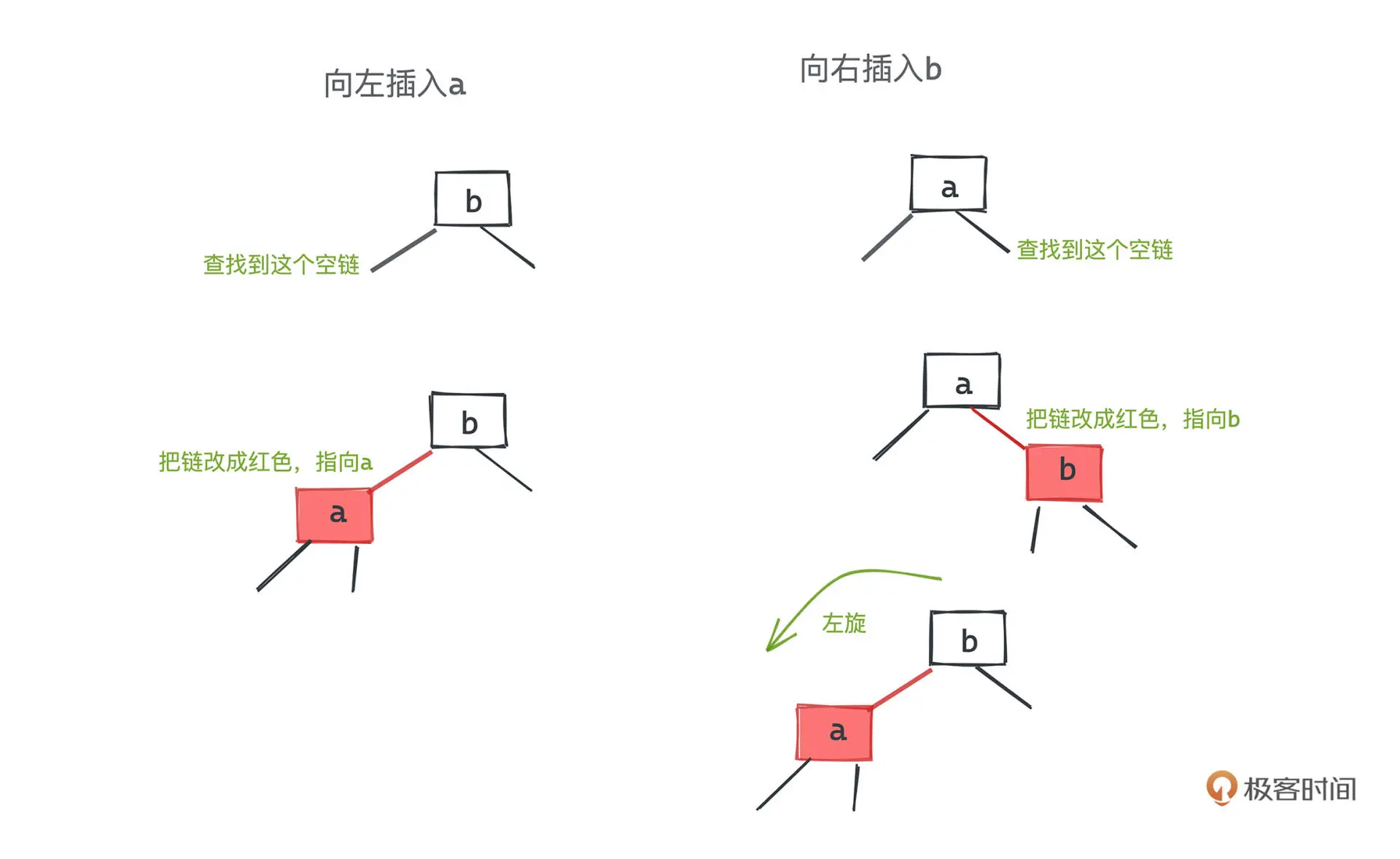
当插入左边时,直接将 2 节点升为 3 节点即可
当插入右边时,将 2 节点提升为不符合规则的 3 节点,然后进行一次左旋即可。
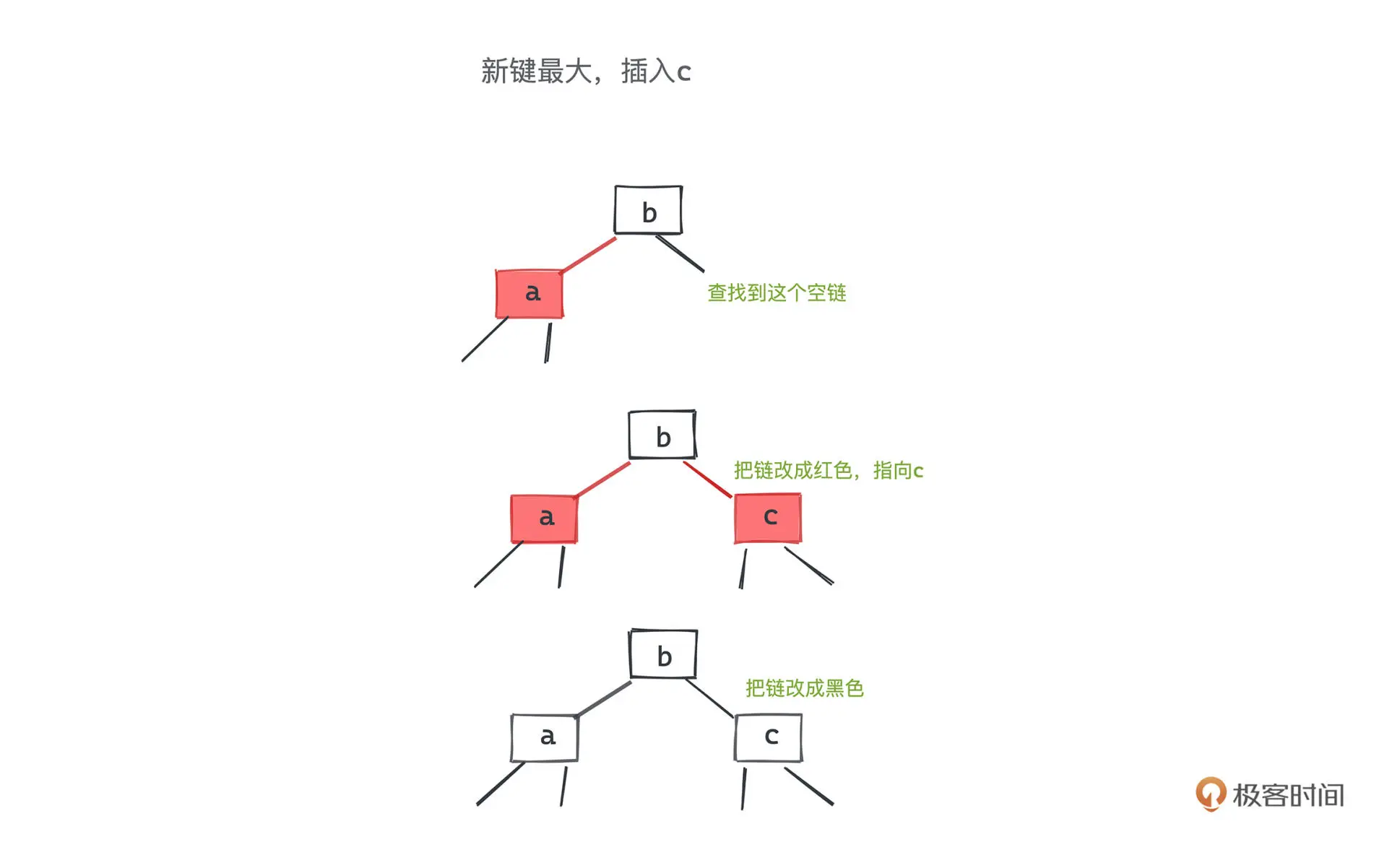
3 节点插入
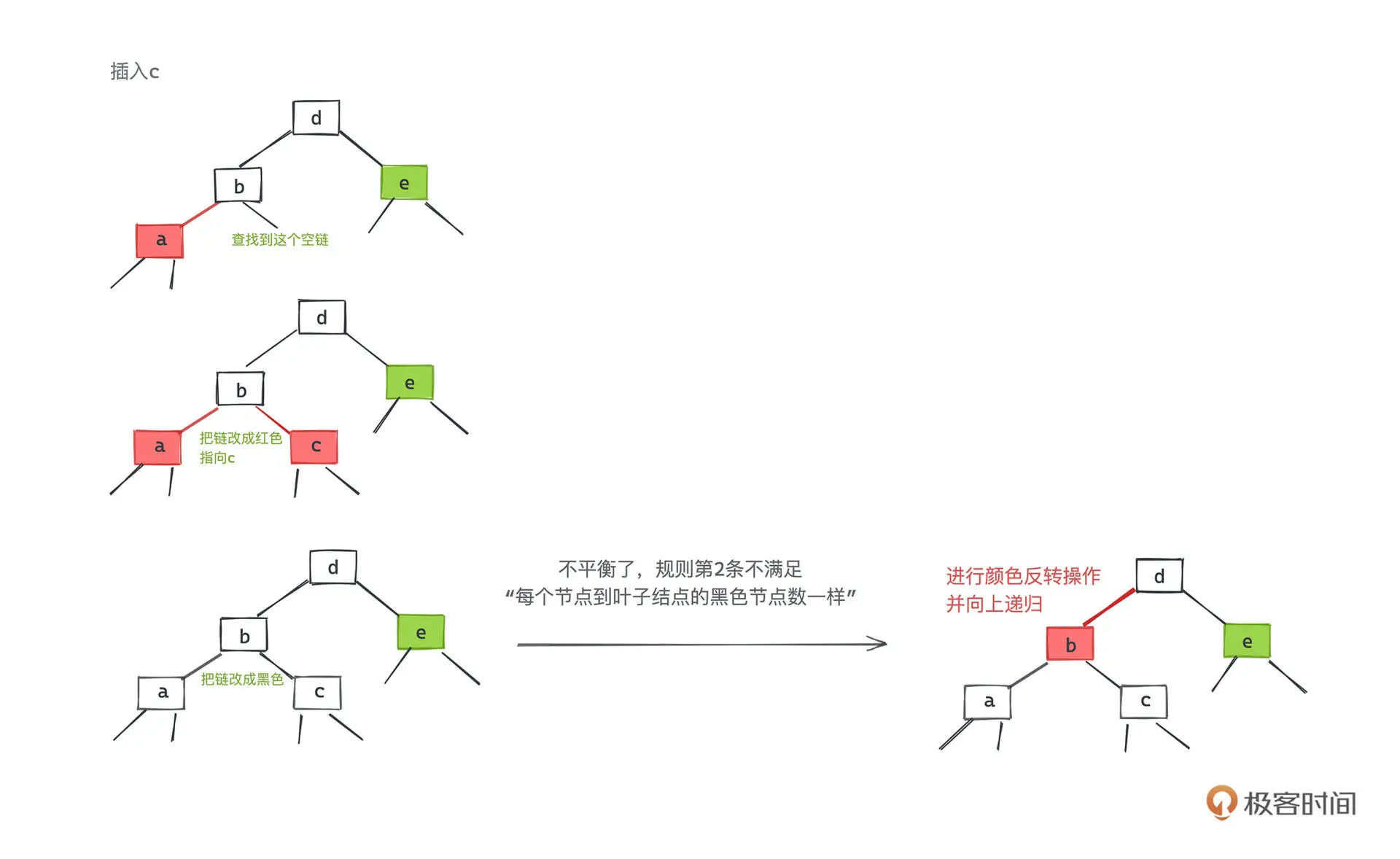
当插入右键的右侧时,将中间节点提升一层,并将左右节点变成黑色
当插入中间或者左侧时,需要进行一到两次的旋转
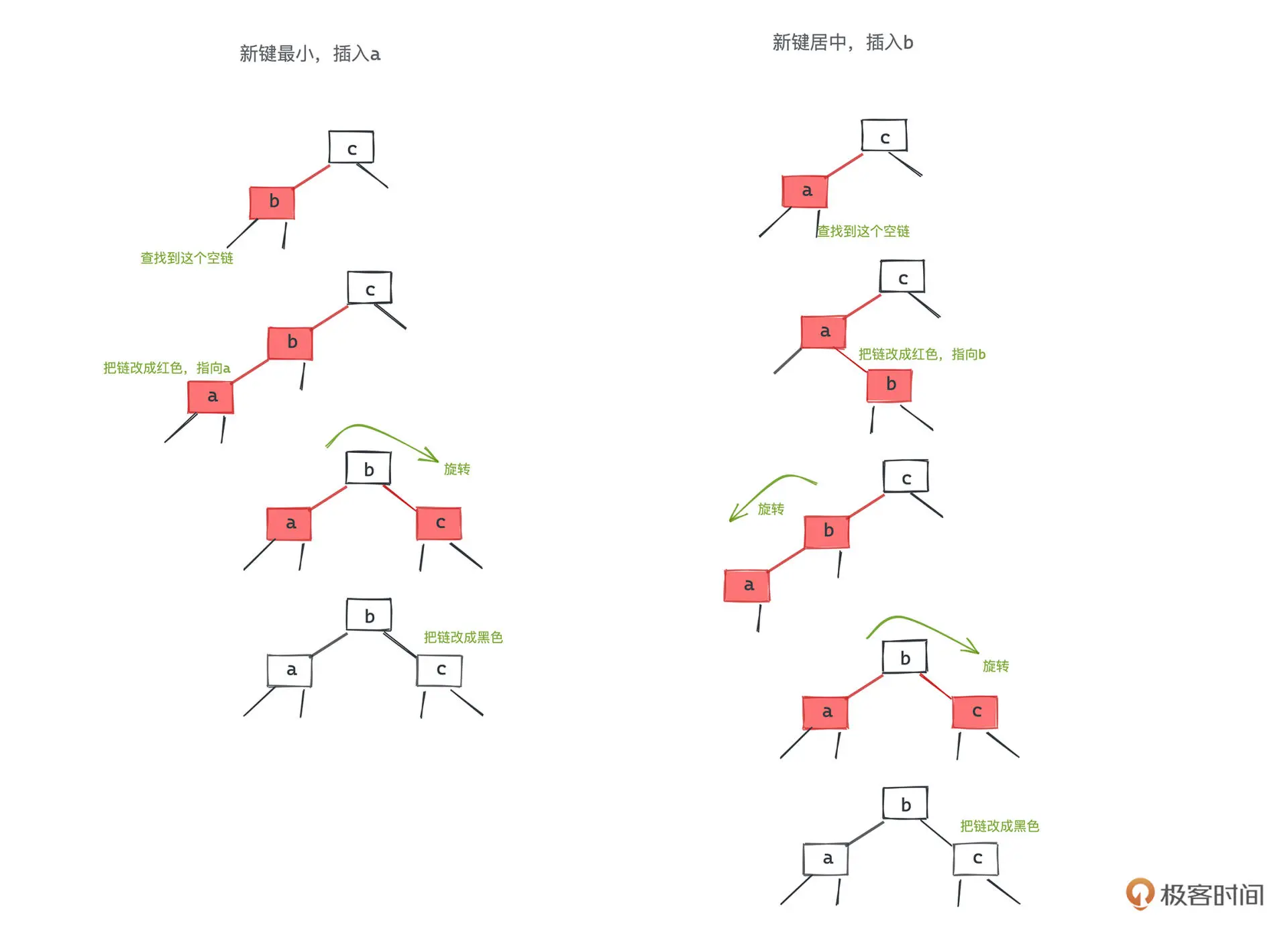
将三节点的左右节点变成黑色后,需要将中间键变成红色,这样当前子树到各个子节点路径的
黑色节点数量就不会变化了
第七讲 堆
优先队列
优先队列中的每一个元素,我们会赋予它一个优先级,优先级相同的元素遵循先进选出的原则
,另有优先级高可以优先出队。
优先队列可以有多种实现方式,如链表、红黑树,但对于出队时找到优先级最高的元素需求,
二叉堆是更好的选择。
二叉堆
二叉堆 binary heap 是建立在二叉树之上的,它有两个约束:
- 二叉堆是一颗满二叉树
- 二叉堆的每个节点和其子节点有偏序关系,大顶堆要求所有节点的值一定大于其左右子树的任何一个节点的值,小顶堆同理。
PriorityQueue 实现
以 JDK 14 的 PriorityQueue (简称 PQ)为例,分析基于堆的具体实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
|
public class PriorityQueue<E> extends AbstractQueue<E>
implements java.io.Serializable {
/**
* Priority queue represented as a balanced binary heap: the two
* children of queue[n] are queue[2*n+1] and queue[2*(n+1)]. The
* priority queue is ordered by comparator, or by the elements'
* natural ordering, if comparator is null: For each node n in the
* heap and each descendant d of n, n <= d. The element with the
* lowest value is in queue[0], assuming the queue is nonempty.
*/
transient Object[] queue; // non-private to simplify nested class access
/**
* The number of elements in the priority queue.
*/
int size;
/**
* Inserts the specified element into this priority queue.
*
* @return {@code true} (as specified by {@link Queue#offer})
* @throws ClassCastException if the specified element cannot be
* compared with elements currently in this priority queue
* according to the priority queue's ordering
* @throws NullPointerException if the specified element is null
*/
public boolean offer(E e) { ... }
/**
* Increases the capacity of the array.
*
* @param minCapacity the desired minimum capacity
*/
private void grow(int minCapacity) { ... }
public E peek() {
return (E) queue[0];
}
/**
* Inserts item x at position k, maintaining heap invariant by
* promoting x up the tree until it is greater than or equal to
* its parent, or is the root.
*
* To simplify and speed up coercions and comparisons, the
* Comparable and Comparator versions are separated into different
* methods that are otherwise identical. (Similarly for siftDown.)
*
* @param k the position to fill
* @param x the item to insert
*/
private void siftUp(int k, E x) { ... }
public E poll() { ... }
}
}
|
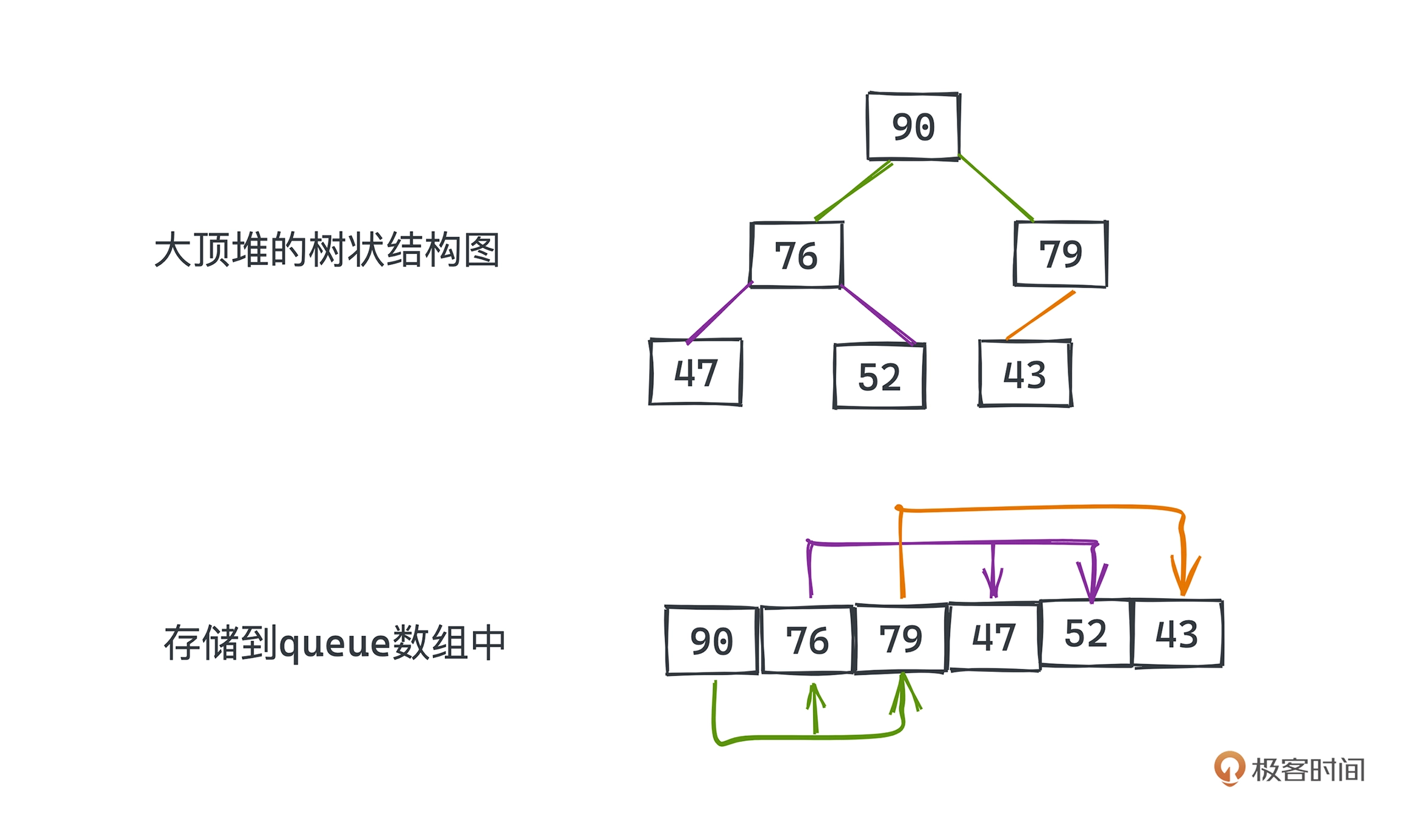
可以看到使用 queue 数组来存放元素,节点 queue[k] 对应的左右节点分别为
queue[2k+1]、queue[2k+2]。
堆的操作
插入
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
/**
* Inserts the specified element into this priority queue.
*
* @return {@code true} (as specified by {@link Queue#offer})
* @throws ClassCastException if the specified element cannot be
* compared with elements currently in this priority queue
* according to the priority queue's ordering
* @throws NullPointerException if the specified element is null
*/
public boolean offer(E e) {
if (e == null)
throw new NullPointerException();
modCount++;
int i = size;
if (i >= queue.length)
grow(i + 1);
siftUp(i, e);
size = i + 1;
return true;
}
|
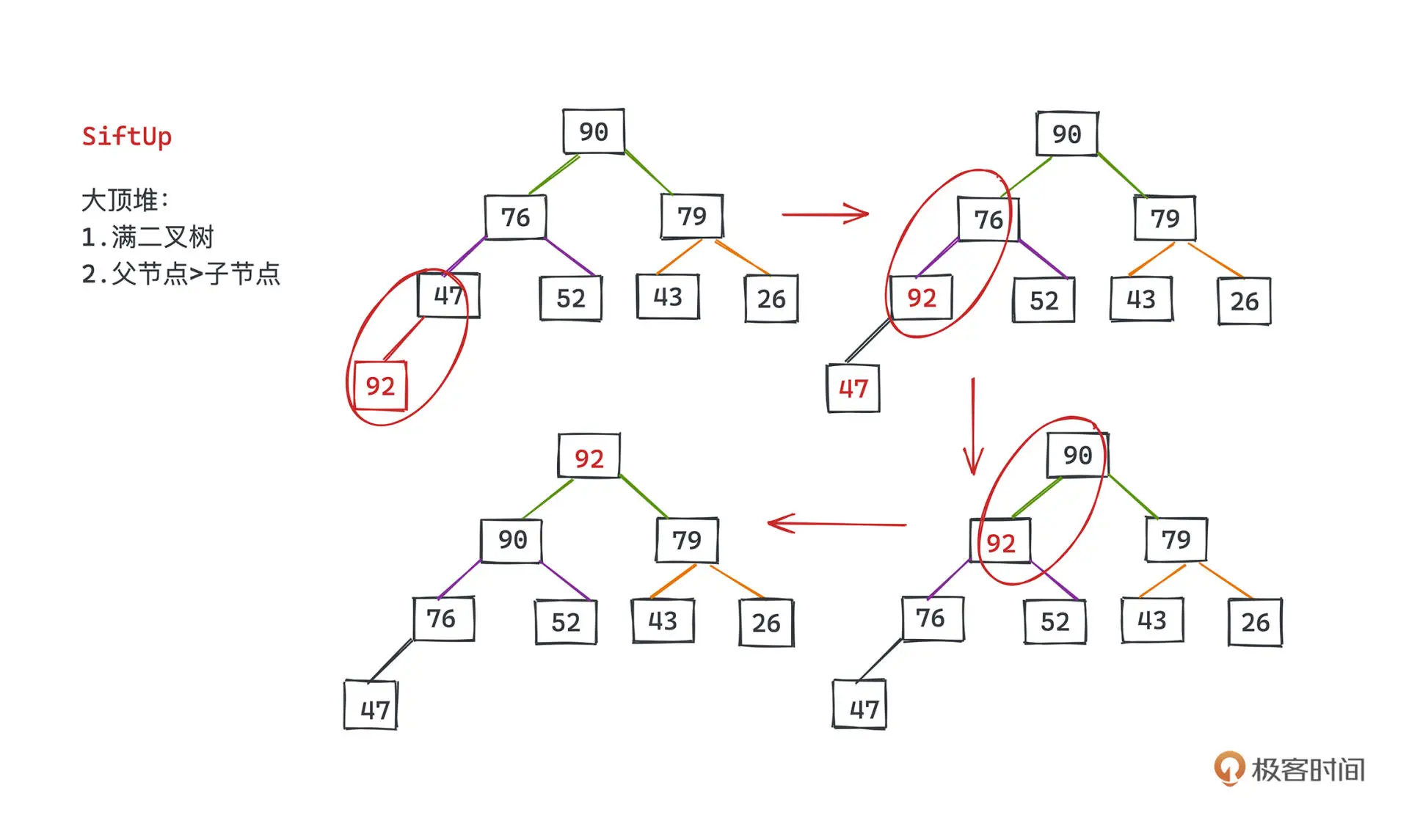
真正的插入操作是在 siftUp 函数中实现的。
首先把元素放在数组尾部,然后依次向上与父节点比较,如果满足条件则位置互换。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
private void siftUp(int k, E x) {
if (comparator != null)
siftUpUsingComparator(k, x, queue, comparator);
else
siftUpComparable(k, x, queue);
}
private static <T> void siftUpComparable(int k, T x, Object[] es) {
Comparable<? super T> key = (Comparable<? super T>) x;
while (k > 0) {
// 计算父节点的下标
int parent = (k - 1) >>> 1;
Object e = es[parent];
// 比较当前节点和父节点的关系 如果当前节点优先级更高,我们可以直接结束比较
if (key.compareTo((T) e) >= 0)
break;
// 交换节点
es[k] = e;
k = parent;
}
es[k] = key;
}
|
删除
删除操作是将返回并删除堆顶元素
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
public E poll() {
final Object[] es;
final E result;
// 取出堆顶元素
if ((result = (E) ((es = queue)[0])) != null) {
modCount++;
final int n;
// 其实就是要将最后一个元素放到顶部
final E x = (E) es[(n = --size)];
// 将最后一个元素置空
es[n] = null;
// 进行siftdown操作
if (n > 0) {
final Comparator<? super E> cmp;
if ((cmp = comparator) == null)
siftDownComparable(0, x, es, n);
else
siftDownUsingComparator(0, x, es, n, cmp);
}
}
return result;
}
|
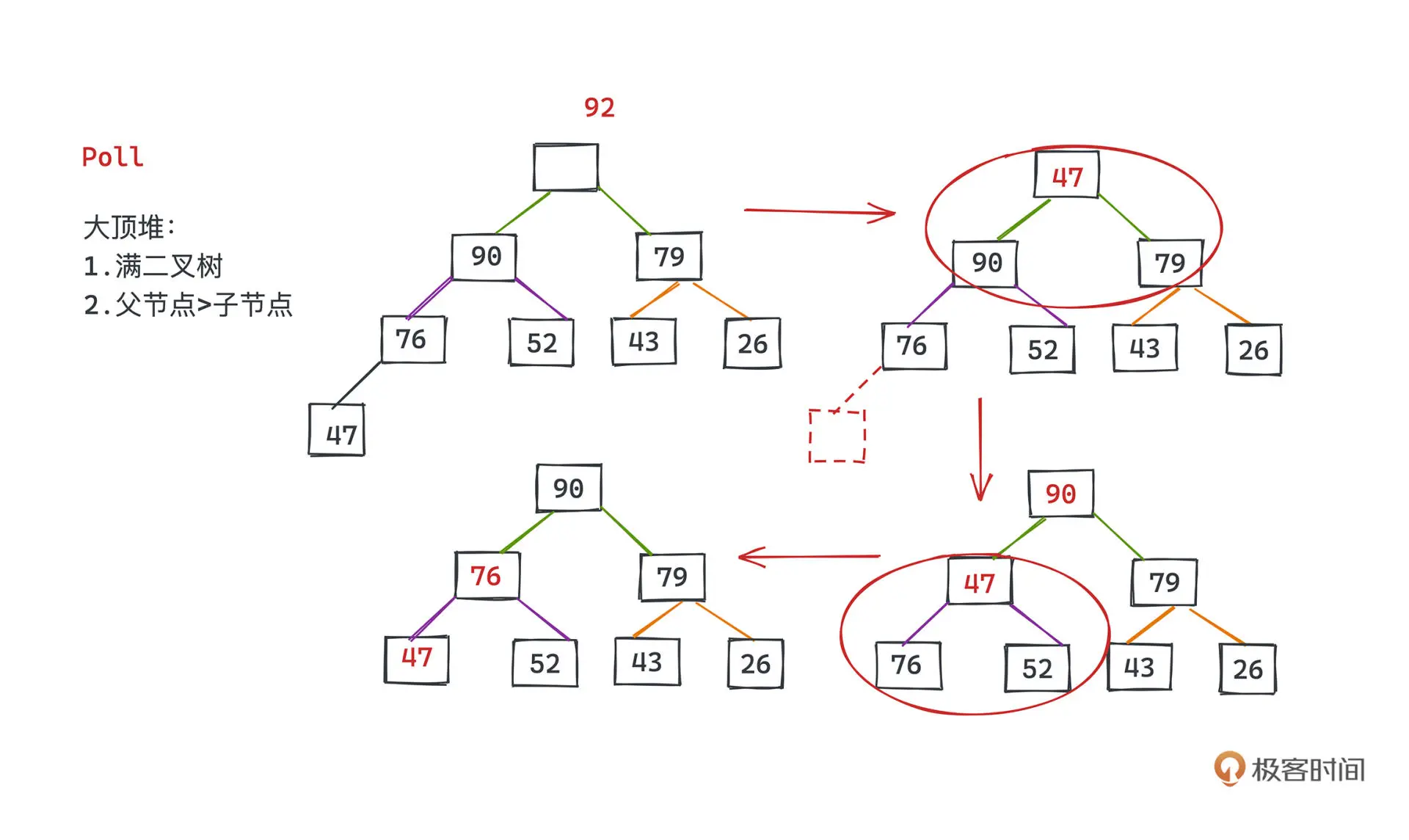
将根节点删除后,我们将尾部的节点提到根节点,然后依次下沉比较交互
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
private static <T> void siftDownComparable(int k, T x, Object[] es, int n) {
// assert n > 0;
Comparable<? super T> key = (Comparable<? super T>)x;
int half = n >>> 1; // loop while a non-leaf
while (k < half) {
int child = (k << 1) + 1; // assume left child is least
Object c = es[child];
int right = child + 1;
if (right < n &&
((Comparable<? super T>) c).compareTo((T) es[right]) > 0)
c = es[child = right];
if (key.compareTo((T) c) <= 0)
break;
es[k] = c;
k = child;
}
es[k] = key;
}
|
扩容
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
/**
* Increases the capacity of the array.
*
* @param minCapacity the desired minimum capacity
*/
private void grow(int minCapacity) {
int oldCapacity = queue.length;
// Double size if small; else grow by 50%
int newCapacity = ArraysSupport.newLength(oldCapacity,
minCapacity - oldCapacity, /* minimum growth */
oldCapacity < 64 ? oldCapacity + 2 : oldCapacity >> 1
/* preferred growth */);
queue = Arrays.copyOf(queue, newCapacity);
}
|
和 vector 扩容思想类似,当原容量小于 64 时,扩容到 2 倍 +2 ,否则 1.5 倍。
第八讲 外部排序
常见排序算法
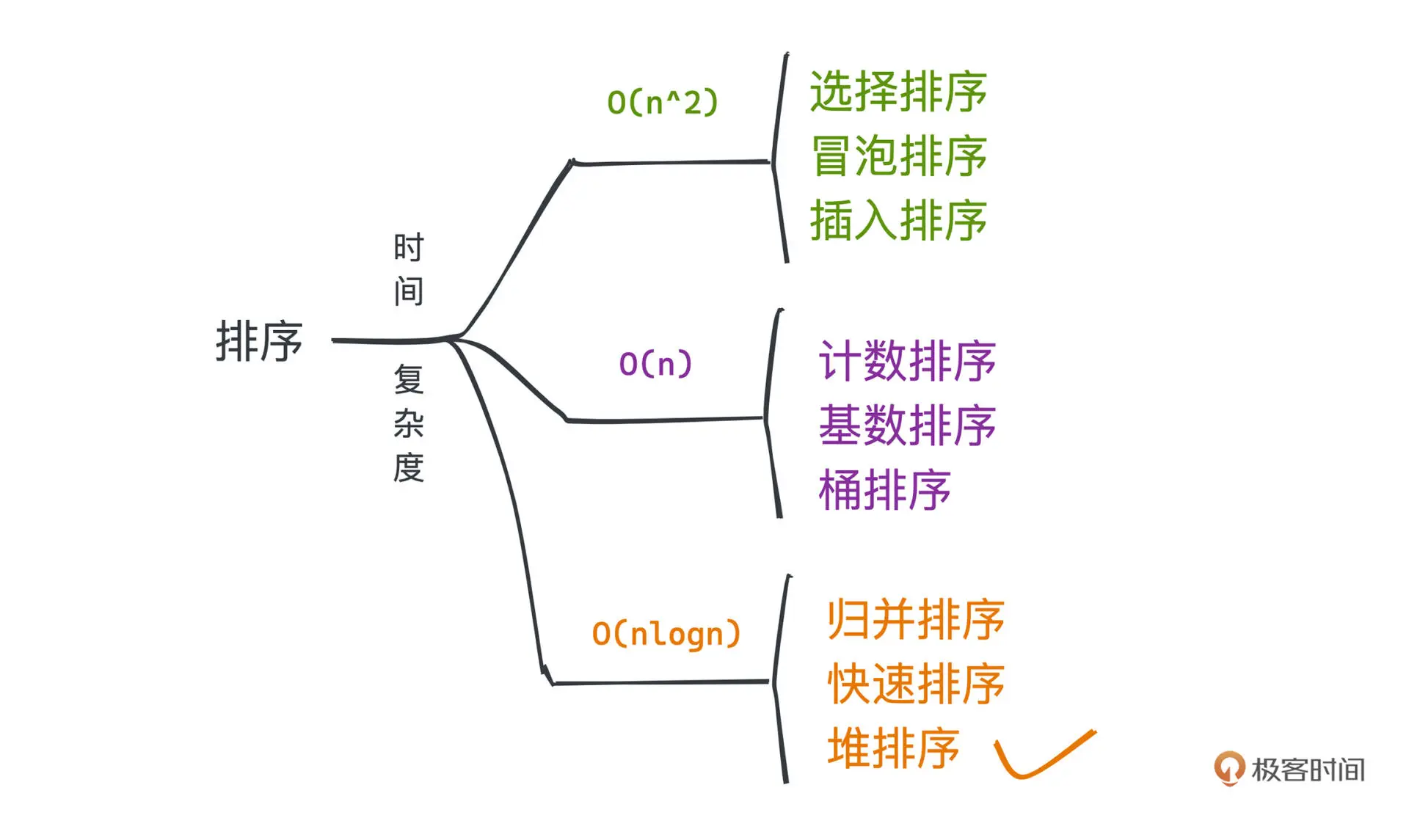
外部排序
外部排序是指借助外部存储来排序,相比内存,外部排序有更大的IO消耗。
常用的外部排序为归并排序。
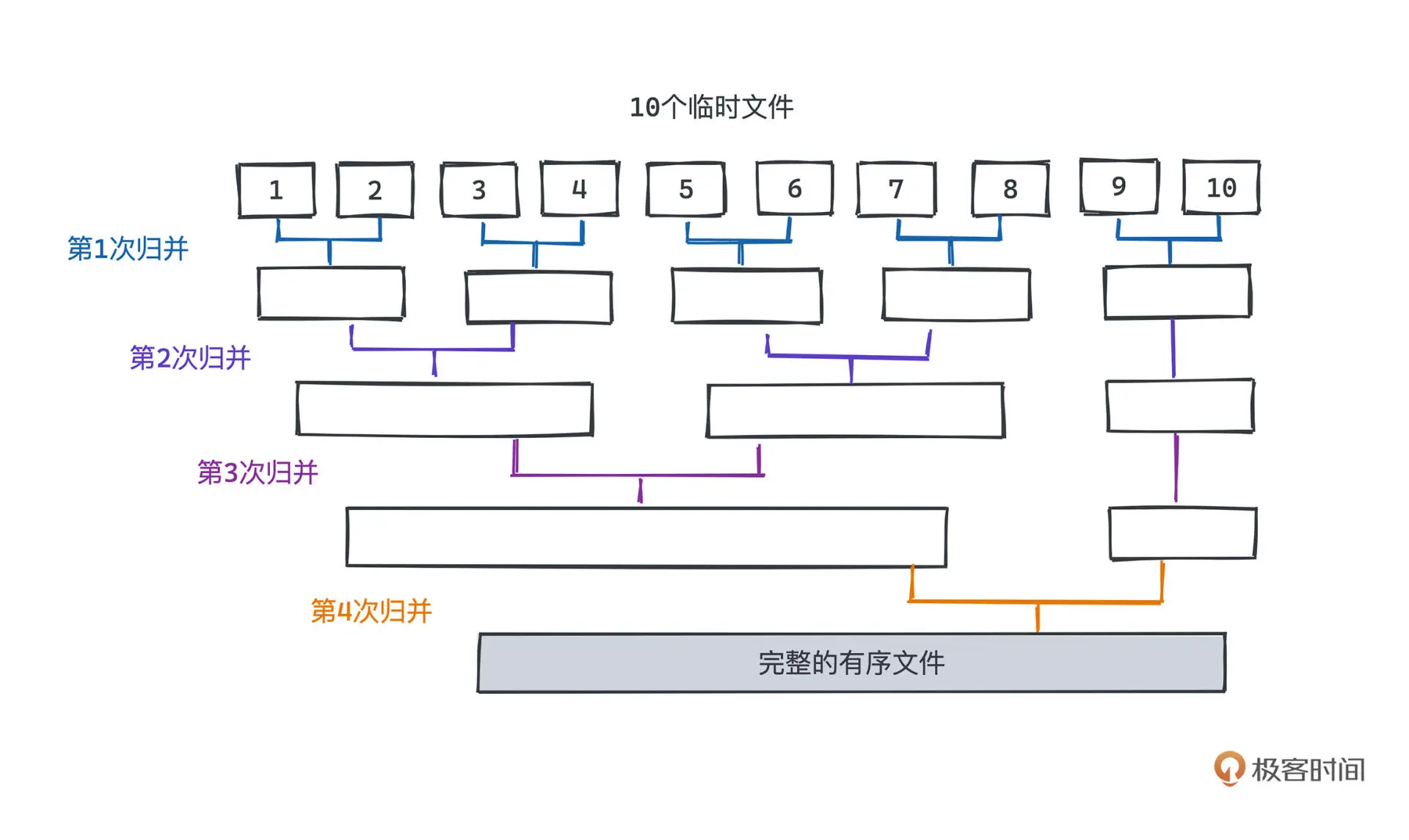
运行时间
每一层我们读取外层的数据总量是一样的,我们要做的是让归并的层次越低越好
假设数据段为 n, 归并路数为 k,那么层数为 logk(n)。
但增加 k 的大小也会导致 从 k 个元素中选择 最小 的元素的代价变高。
败者树
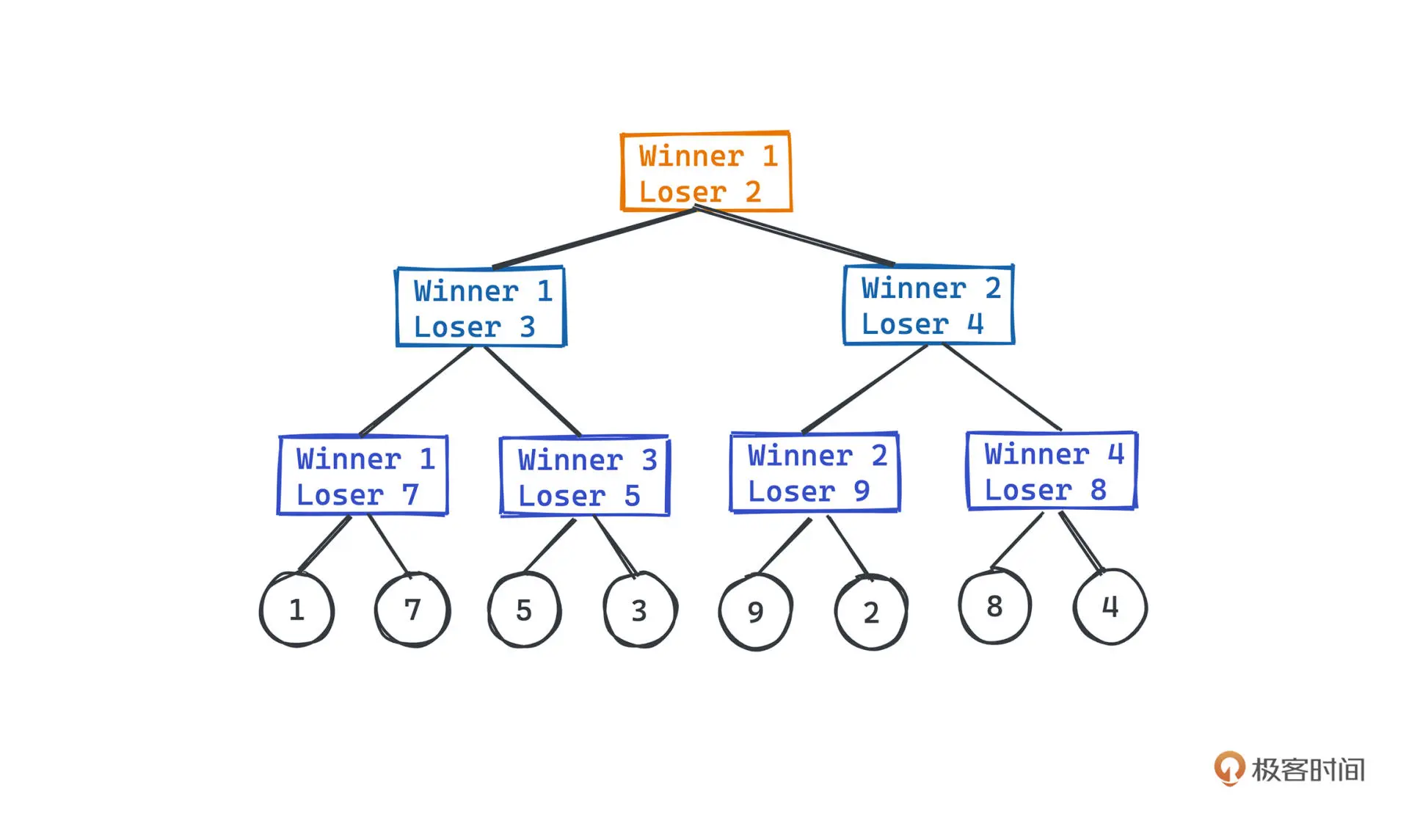
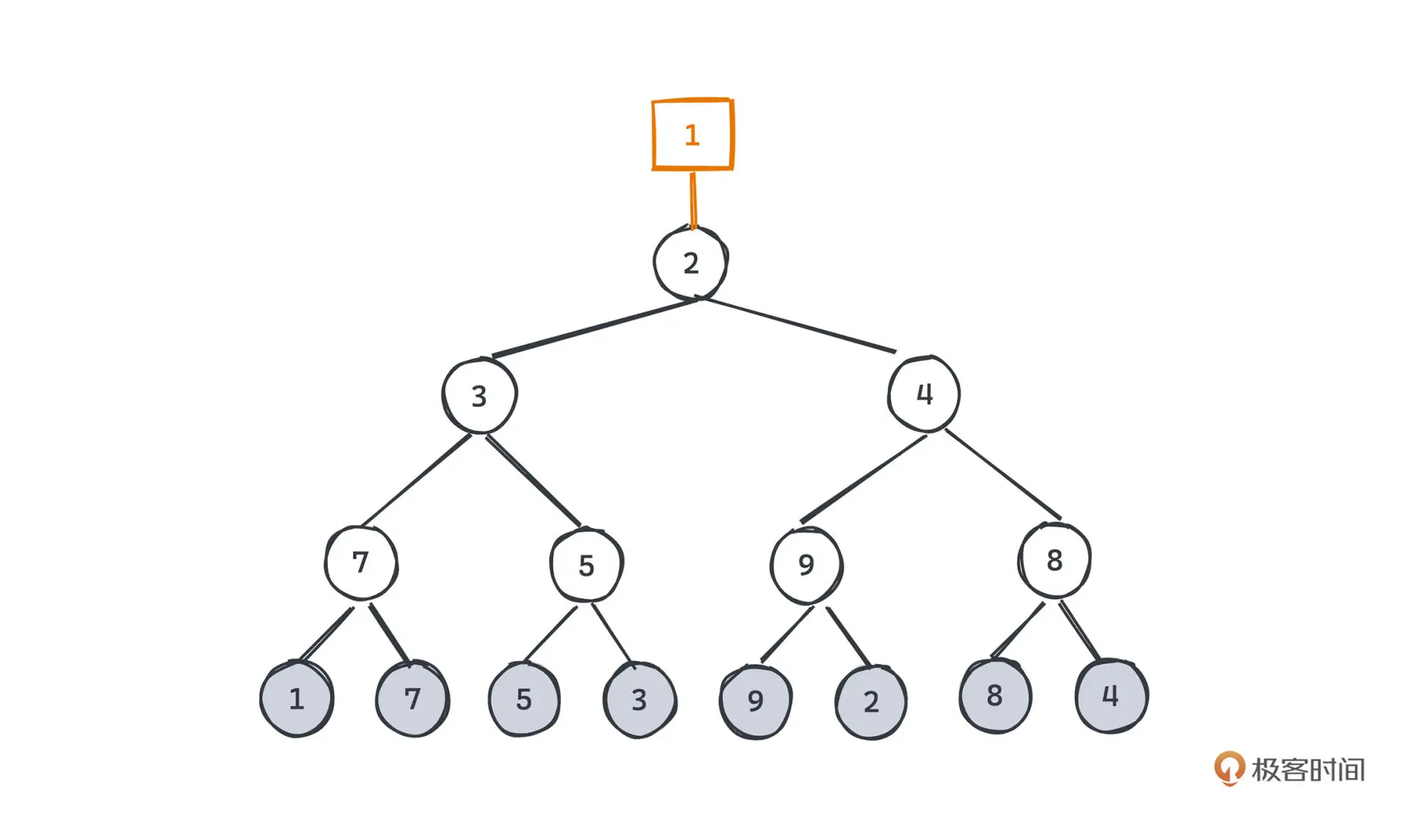
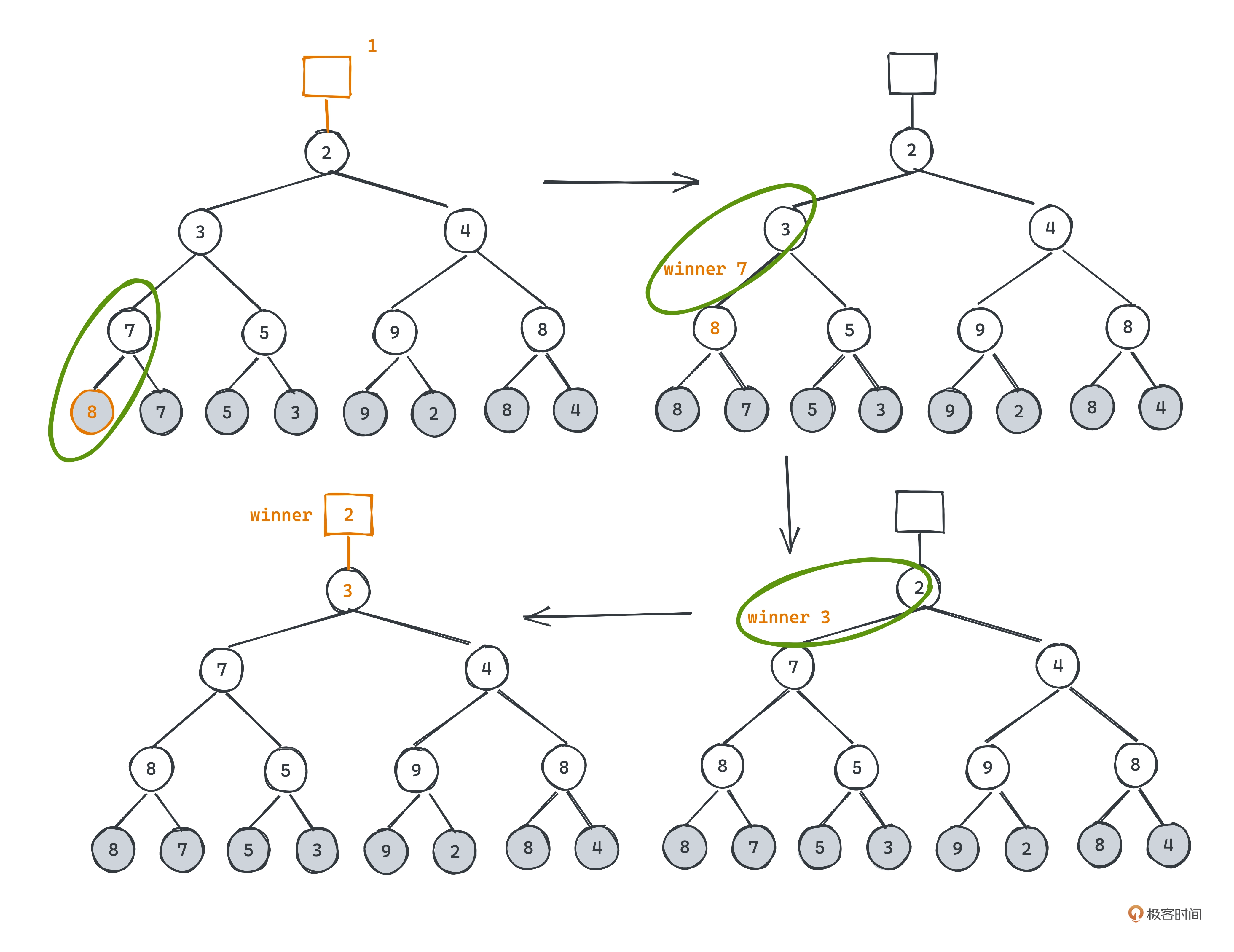
败者树的思想是使用叶子节点存储待比较的元素,两两比较,在父节点存储失败者,然后
对获胜的元素两两比较,得到更上层的失败者。
根节点之上有一个最终获胜者
对于取出胜者并添加新元素的操作,只需要将新元素置于胜者的位置 ,再依次向上比较即可。
败者树相比堆,Pop时只需要和上层的败者比较即可,不像堆一定要和左右子树比较两次。
相关算法题 - 合并K个有序链表
第九讲 二分法
二分查找
二分查找的核心是查找元素和比较有序排列
Kafka
Kafka 中所有的消息都是以"日志"的形式存储,消息按写入时间顺序,依次追加在许多日志文件中。
文件中每条消息会相对第一条消息有一个偏移量(类似自增ID)。
Kafka 每个 topic 会有多个 partition,每个 partition下 的日志按照顺序分成一个个有序日志段。
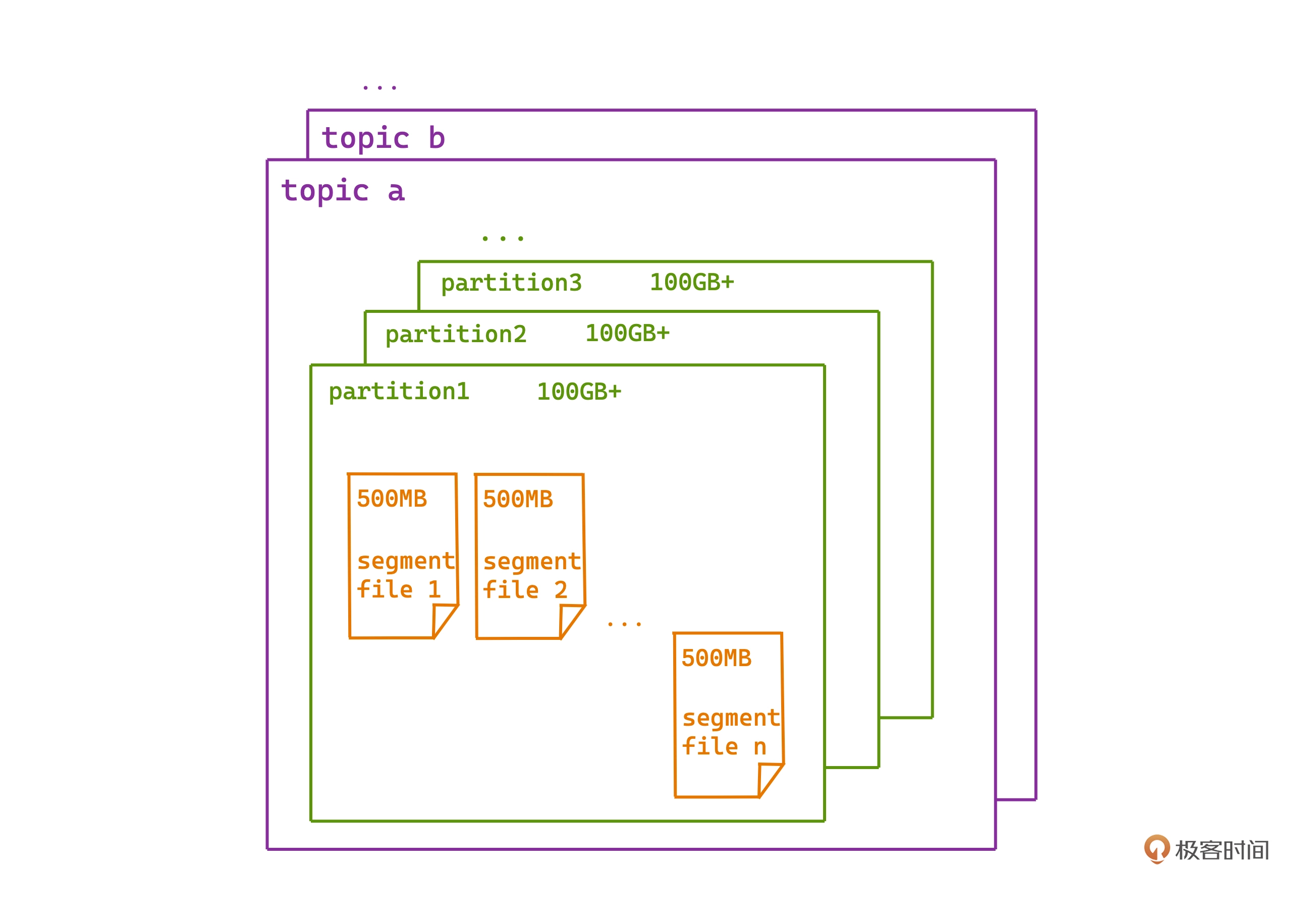
消息查找
1
2
3
4
5
6
|
00000000000000000000.log
00000000000000000000.index
00000000000000000000.timeindex
00000000000000000035.log
00000000000000000035.index
00000000000000000035.timeindex
|
上面为一个典型的日志文件存储情况:
- .log 文件存储的就是消息本身的日志文件
- .index 文件是索引文件
- .timeindex 文件是基于时间戳的索引文件
.index 文件内容示例如下图
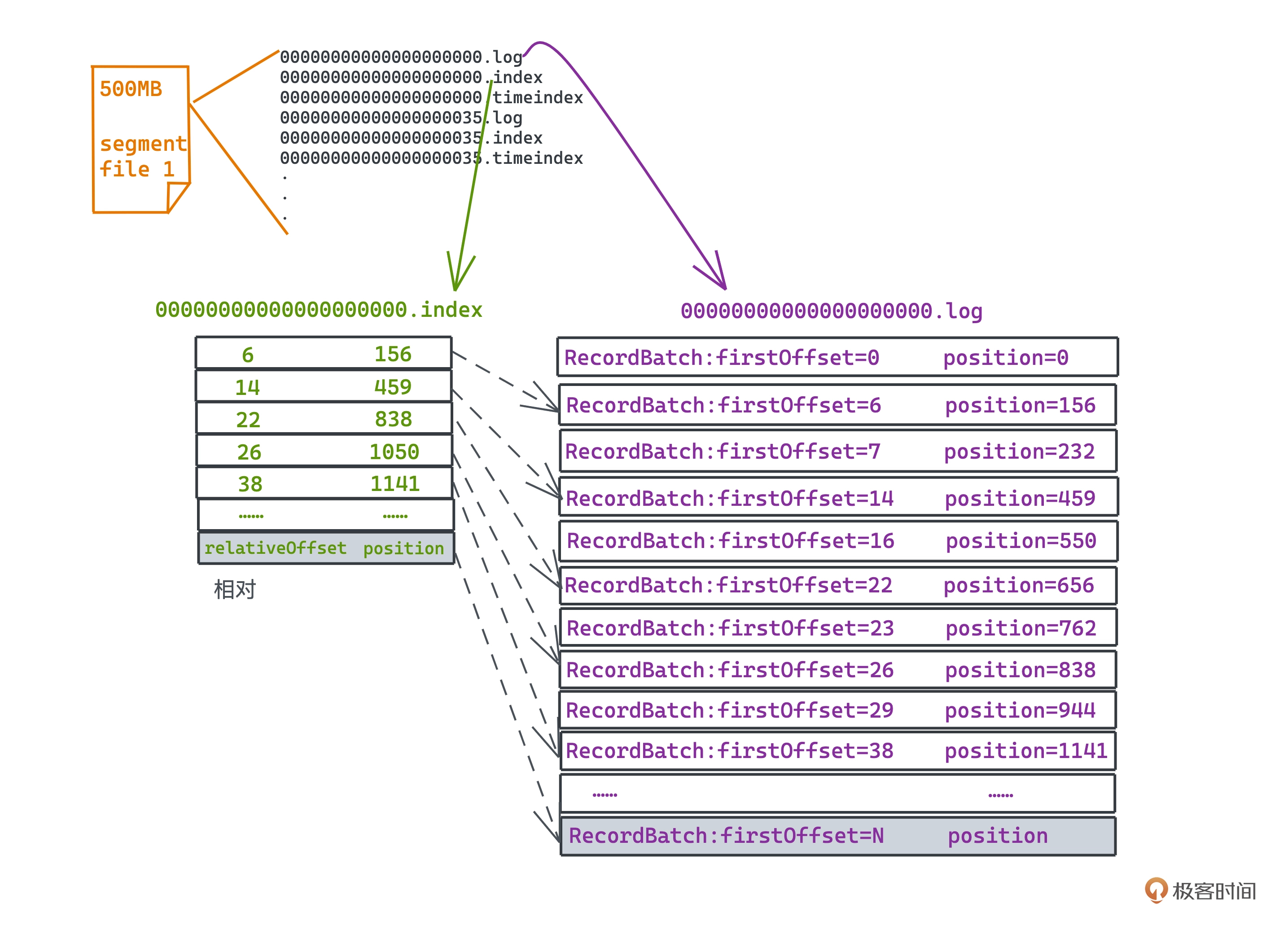
kafka为了使用更小的内存空间,采用了稀疏索引。
源码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
/**
* Lookup lower and upper bounds for the given target.
*/
private def indexSlotRangeFor(idx: ByteBuffer, target: Long, searchEntity: IndexSearchEntity): (Int, Int) = {
// 检查index是否为空
if(_entries == 0)
return (-1, -1)
// 二分搜索
def binarySearch(begin: Int, end: Int) : (Int, Int) = {
var lo = begin
var hi = end
while(lo < hi) {
val mid = ceil(hi/2.0 + lo/2.0).toInt
val found = parseEntry(idx, mid)
val compareResult = compareIndexEntry(found, target, searchEntity)
if(compareResult > 0)
hi = mid - 1
else if(compareResult < 0)
lo = mid
else
return (mid, mid)
}
(lo, if (lo == _entries - 1) -1 else lo + 1)
}
val firstHotEntry = Math.max(0, _entries - 1 - _warmEntries)
// 查询的目标offset是否在热区
if(compareIndexEntry(parseEntry(idx, firstHotEntry), target, searchEntity) < 0) {
return binarySearch(firstHotEntry, _entries - 1)
}
// 查询的目标offset是否小于最小的offset
if(compareIndexEntry(parseEntry(idx, 0), target, searchEntity) > 0)
return (-1, 0)
return binarySearch(0, firstHotEntry)
}
|
Kafka 使用了 mmap 将磁盘文件和内存进行映射, 消息队列的特性决定了
大部分索引查询其实都是在日志比较靠近尾部的区域,将索引中最后 8KB
认为热区,查询是优先查热区,没有命中再查冷区,这样就可以减少缺页中断的次数。
kafka 采用冷热二分查询的改进见这个issue
第十讲 暴力搜索算法
BFS 和 DFS 是两种常见的搜索算法
第十一讲 字符串匹配
Brute-Force 算法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
/*
* s: 主串
* p:模式串
*/
std::vector<int> match(string s, string p) {
std::vector<int> ans;
int n = s.size();
int m = p.size();
int i, j;
for (i = 0; i < n - m + 1; i++) {
for (j = 0; j < m; j++) {
if (s[i + j] != p[j]) break;
}
if (j == m) ans.push_back(i);
}
return ans;
}
|
Boyer-Moore 算法
坏字符规则
BM 算法采用从后向前匹配的方式
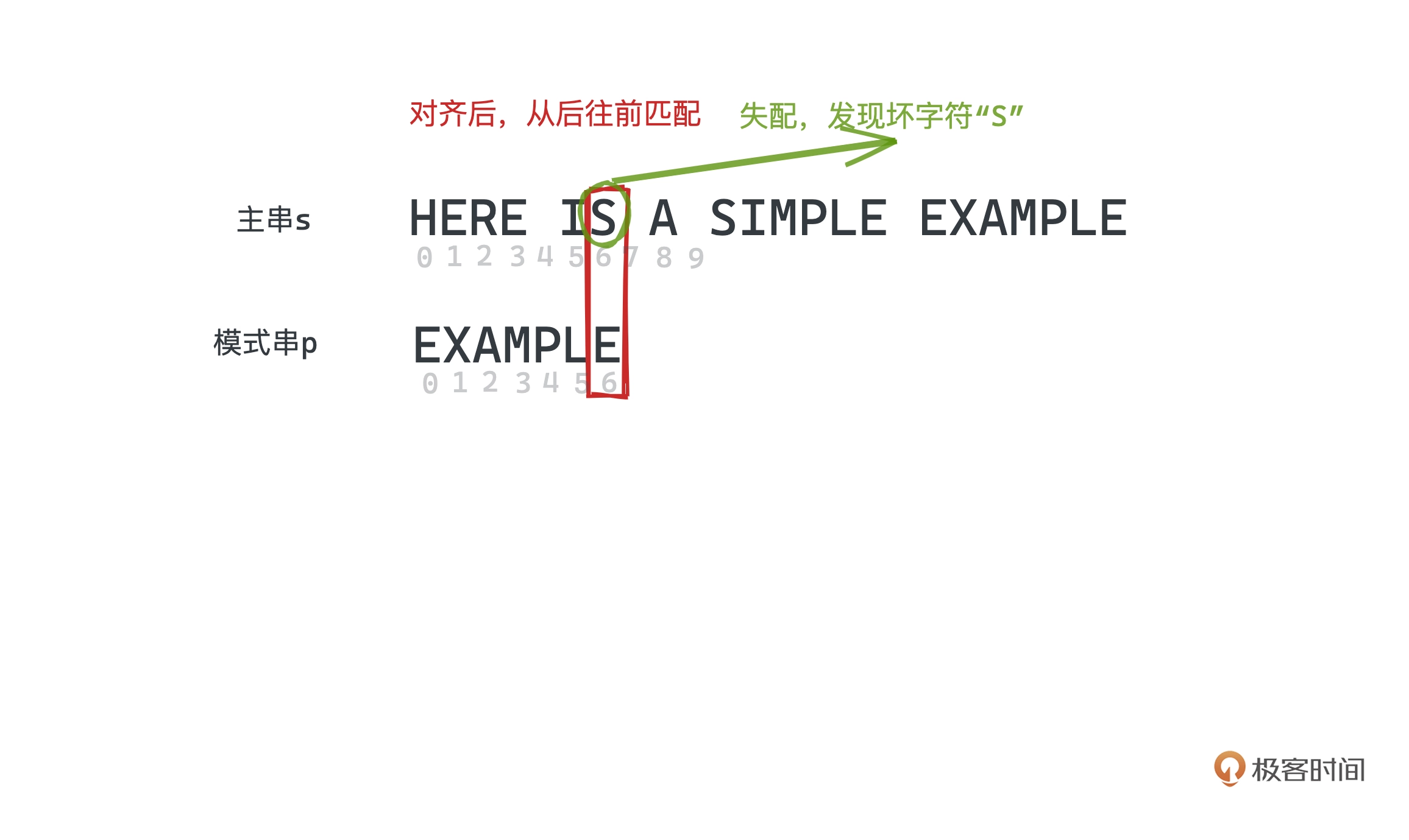
如上图, 位置 6 匹配,那这里的 “S” 就是是个坏字符,遇到坏字符时,
如果在模式串中没有出现,则说明没有重叠,可以直接跳过这段。
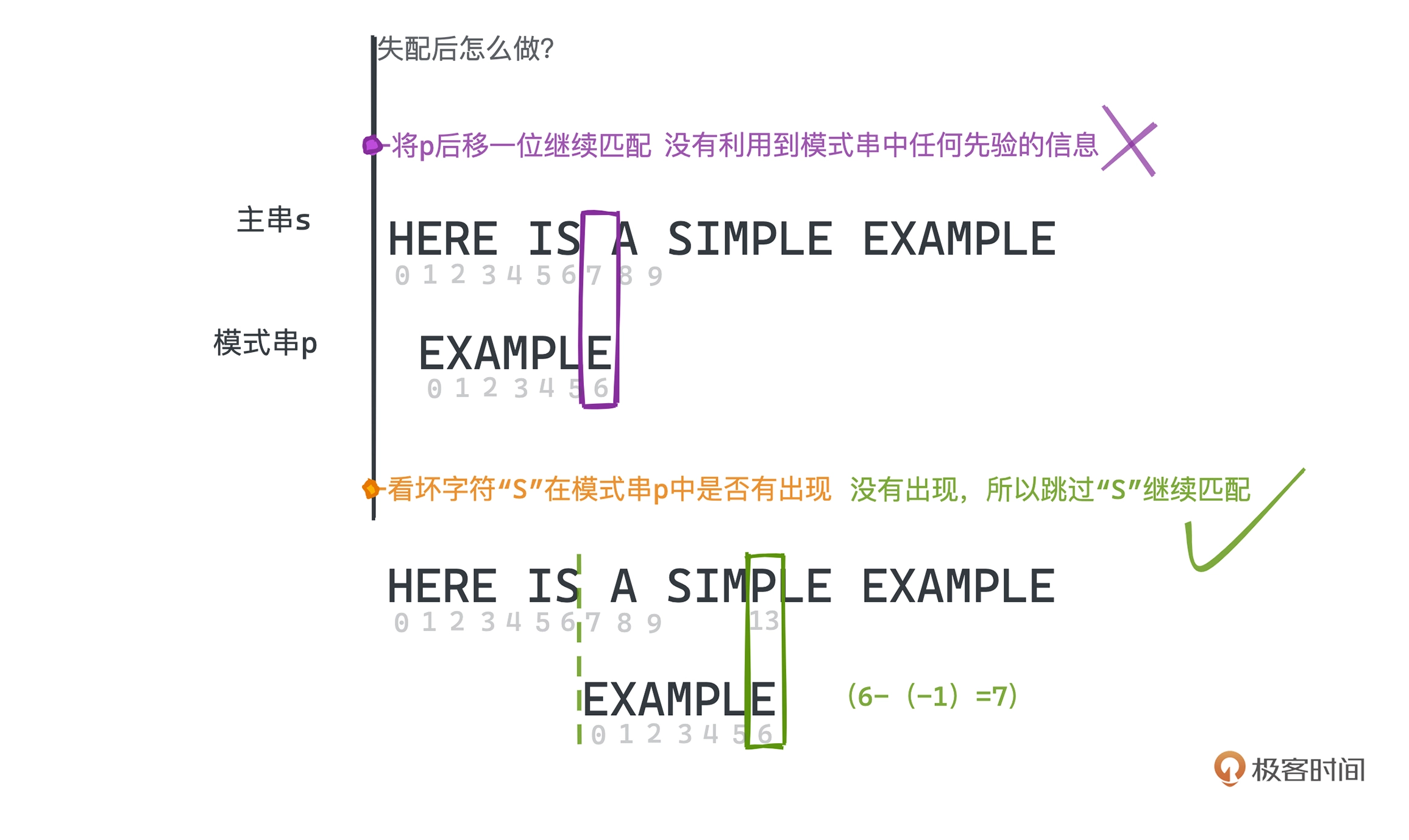
下一步匹配时,发现坏字符"P",但 “P” 在模式串有出现,可以将模式串最后一次出现 “P"的位置对齐
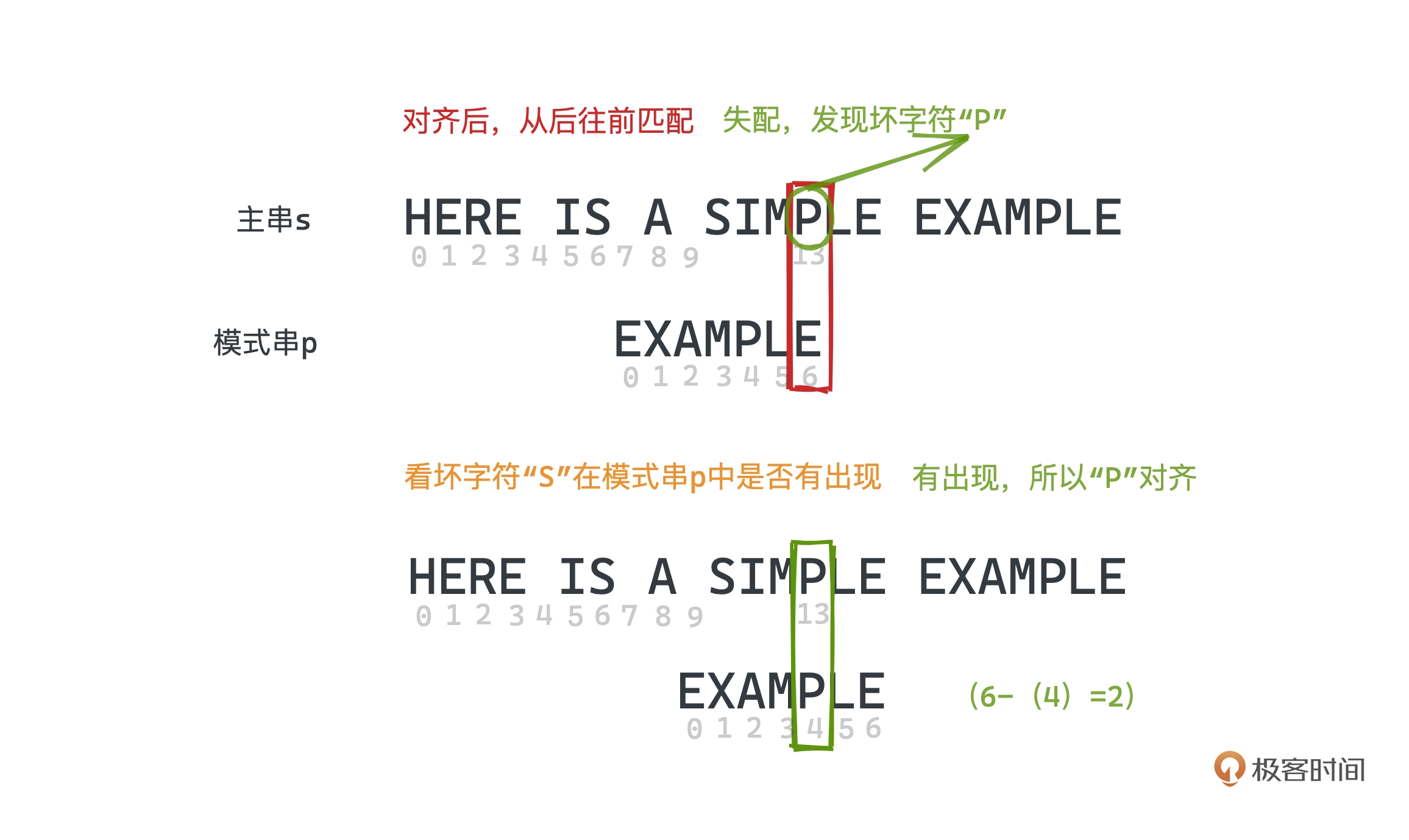
每次发现坏字符时,我们需要向右移动移动 (失配位置 - 失配字符最右出现的下标)位,其中如果失配字符没有在模式串出现,则下标为 -1,
好后缀规则
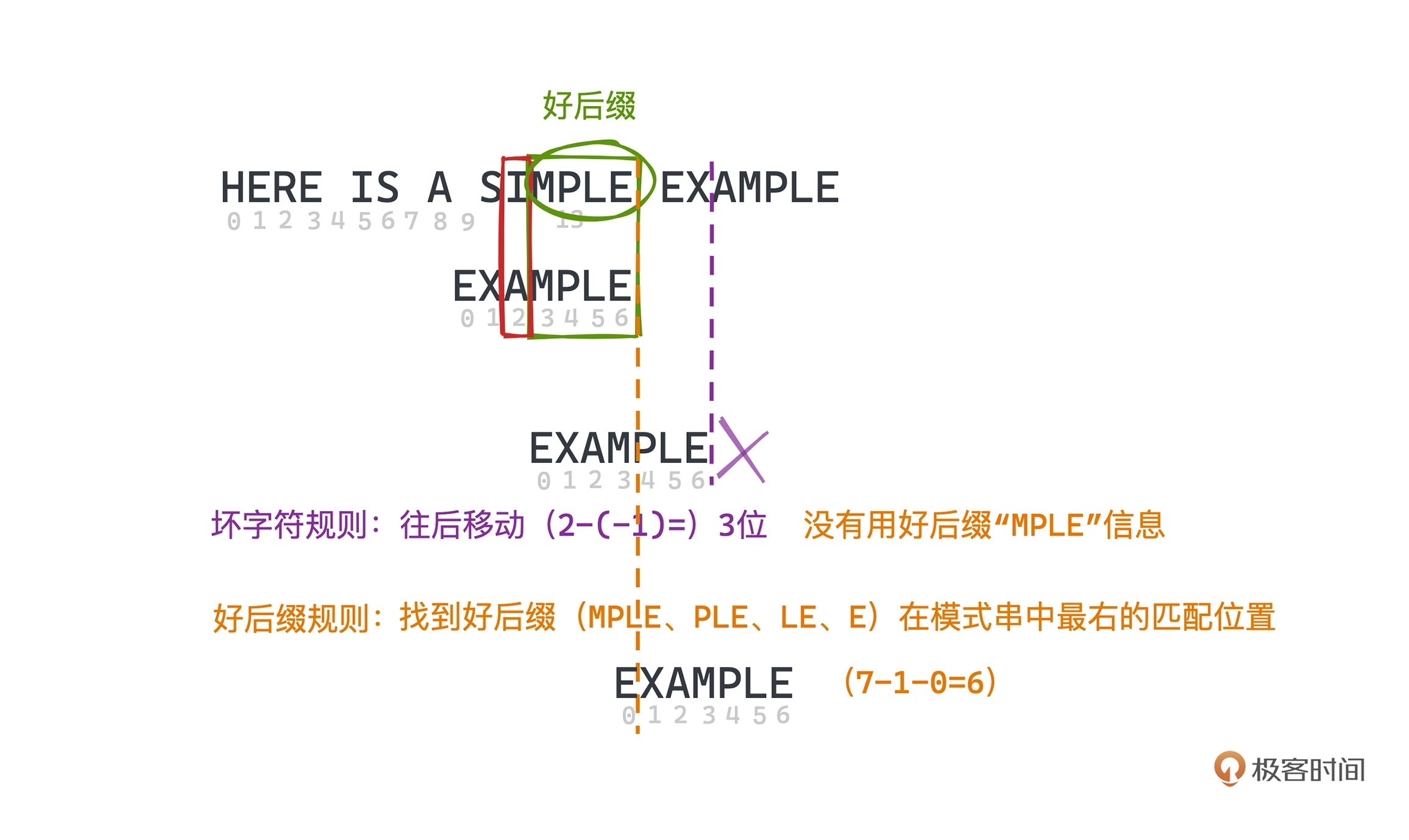
在 SIMPLE 和 EXAMPLE 的匹配中,我们发"MPLE"都匹配得上,那"MPLE"就称之为好后缀,
同样"PLE”、“LE”、“E” 都是好后缀。
如果用坏字符规则,则应该将模式串移动(2 - (-1)) = 3 位,因为"I" 在模式串不存在。
我们使用好后缀的规则: 找到好后缀在模式串中最右的匹配位置,总计向后移动(模式串字符串长度 - 1 - 好后缀在模式串上次出现的位置)位。
上图好后缀"E" 的计算值为 6 (7-1-0)位
BM 算法具体实现
坏字符最右位置计算
1
2
3
4
5
6
|
def get_bc(pattern):
bc = dict() # 记录每个badchar最右出现的位置
for i in range(len(pattern) - 1):
char = pattern[i]
bc[char] = i + 1
return bc
|
我们用 dict 来记录每个字符最右侧位置。工业级的实现会用 [0, 256] 的数组替代来提高性能。
好后缀计算
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
def get_gs(pattern):
gs = dict()
gs[''] = len(pattern)
# suf_len 用于标记后缀长度
for suf_len in range(len(pattern)):
suffix = pattern[len(pattern) - suf_len - 1:]
# j 用于标记可用于匹配的位置
for j in range(len(pattern) - suf_len - 1):
substr = pattern[j:j + suf_len + 1]
if suffix == substr:
gs[suffix] = len(pattern) - j - suf_len - 1
for suf_len in range(len(pattern)):
suffix = pattern[len(pattern) - suf_len - 1:]
if suffix in gs: continue
gs[suffix] = gs[suffix[1:]]
gs[''] = 0
return gs
|
匹配
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
def bm(string, pattern, bc, gs):
# i 用于标记当前模式串和主串哪个位置左对齐。
i = 0
# j 用于标记当前模式串匹配到哪个位置;从右往左遍历匹配。
j = len(pattern)
while i < len(string) - len(pattern) and (j > 0):
# 从右往左匹配每个位置
a = string[i + j - 1]
b = pattern[j - 1]
if a == b: # 匹配的上,继续匹配前一位
j = j - 1
else: # 匹配不上,根据两个规则的预处理结果进行快速移动
i = i + max(gs.setdefault(pattern[j:], len(pattern)), j - bc.setdefault(a, 0))
j = len(pattern)
# 匹配成功返回匹配位置
if j == 0:
return i
# 匹配失败返回 None
return -1
if __name__ == '__main__':
string = 'here is a simple example '
pattern = 'example'
bc = get_bc(pattern) # 坏字符表
gs = get_gs(pattern) # 好后缀表
print(gs)
x = bm(string, pattern, bc, gs)
print(x)
|
第十二讲 拓扑排序
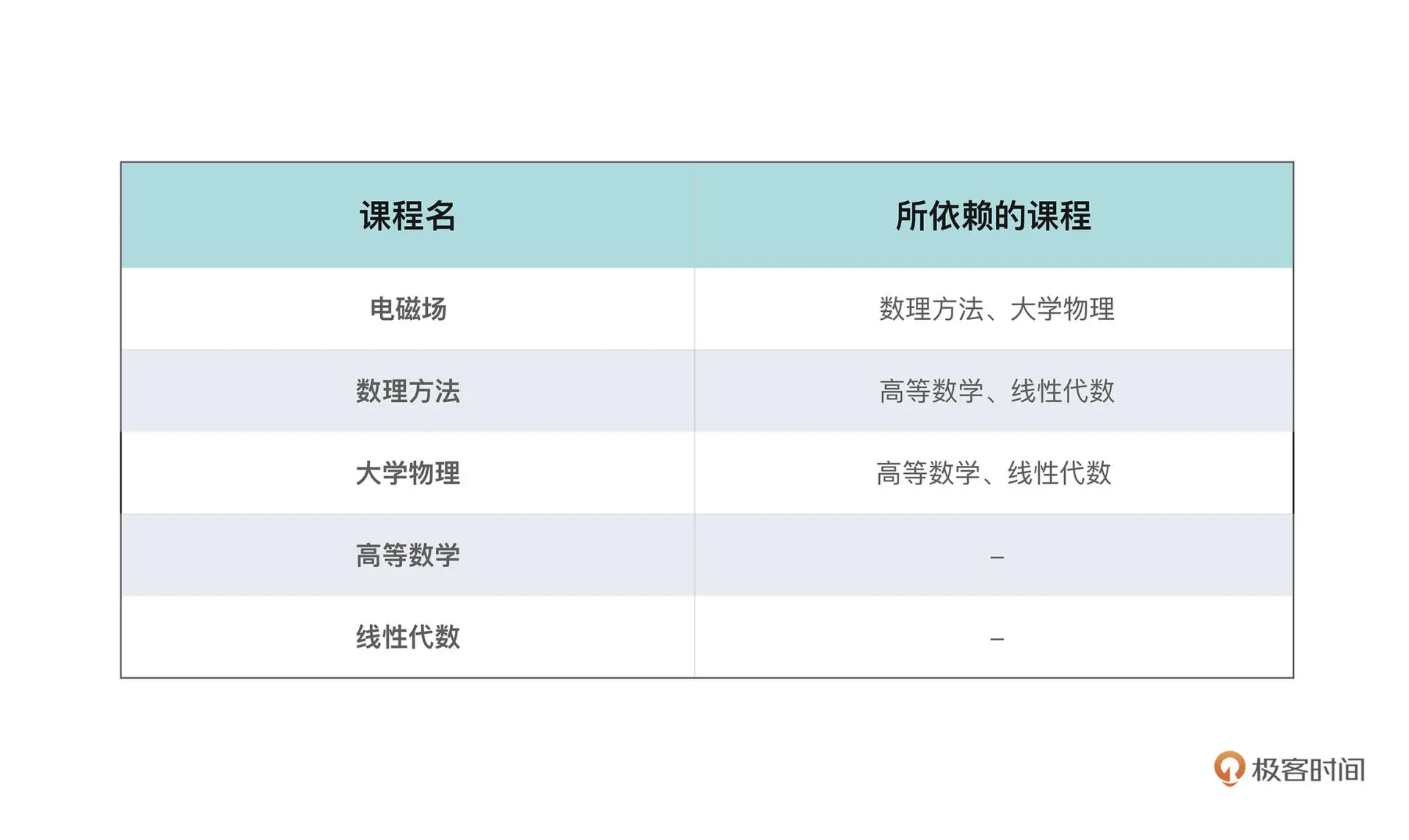
如上图的课表,部分课程学习有一些前置课程,用图的方式表示如下:
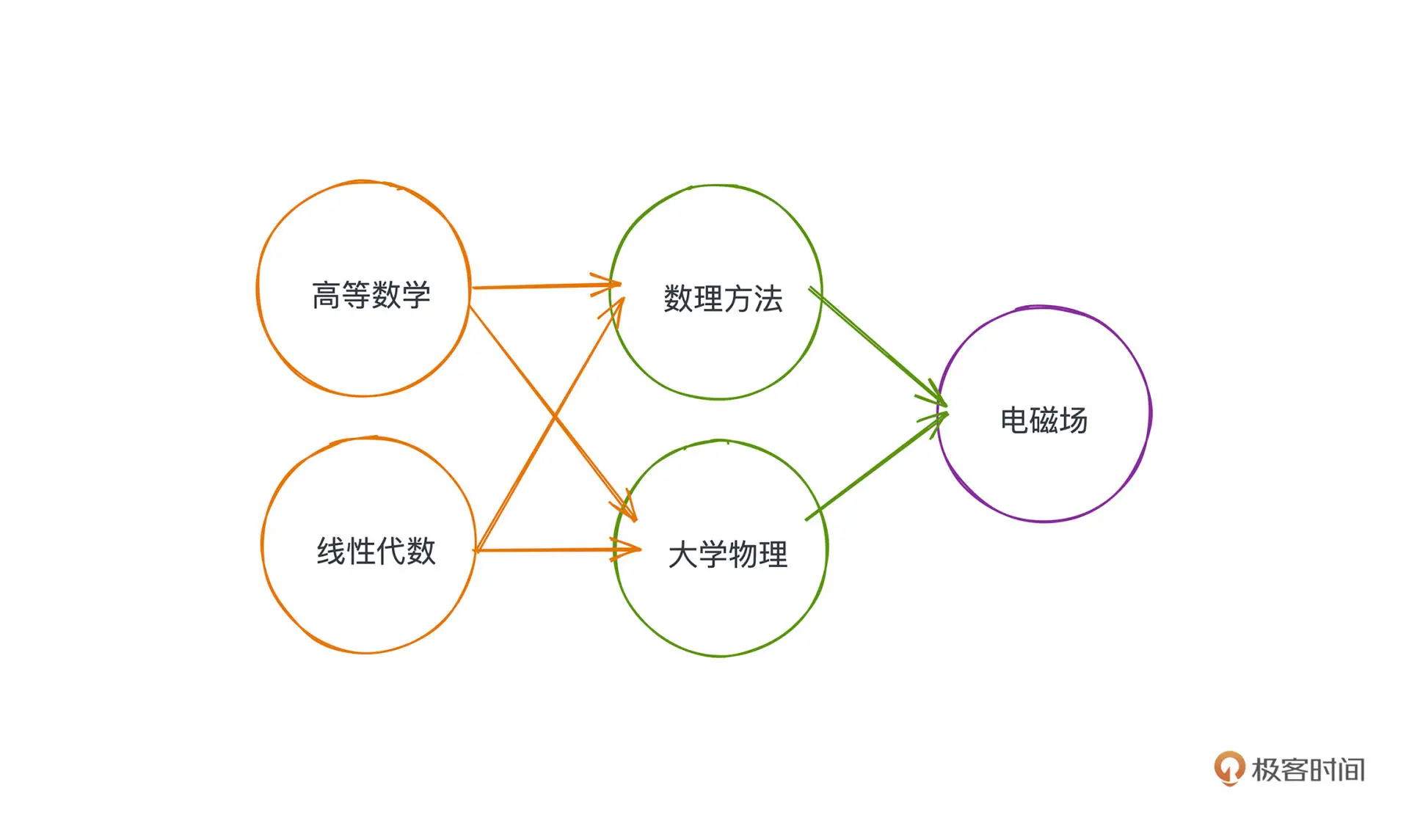
如果我们给出一个序列使得每个节点只出现一次,且保证如果存在路径 P 从 A 到 B,
那么 A 在序列中一定出现在 B 之前,满足这个条件的序列就被可认为满拓扑排序。
拓扑排序是建立在有向无环图(DAG)的基础之上的.
khan 算法
khan 算法是一种基于贪心和广度优先思想的拓扑排序实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
|
class Solution {
public:
vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
// 邻接表数组
vector<vector<int>> next(numCourses, vector<int>());
// 入度表
vector<int> pre(numCourses, 0);
// 标记是否遍历过
vector<int> visited(numCourses, 0);
// 记录最终修读顺序
vector<int> ans;
// 构图
for (auto edge: prerequisites) {
int n = edge[0];
int p = edge[1];
next[p].push_back(n);
pre[n]++;
}
queue<int> q;
// 所有没有先修课程的课程入队
for (int i = 0; i < numCourses; i++) {
if (pre[i] == 0) {
q.push(i);
}
}
// BFS搜索
while(!q.empty()) {
int p = q.front();
q.pop();
ans.push_back(p);
visited[p] = 1;
// 遍历所有以队首课程为先修课程的课程
for (auto n: next[p]) {
// 由于队首课程已经被修读,所以当前课程入度-1
pre[n]--;
// 如果该课程所有先修课程已经修完;将该课程入队
if (pre[n] == 0) {q.push(n);}
}
}
// 环路检测: 如果仍有课程没有修读;说明环路存在
for (int i = 0; i < numCourses; i++) {
if (!visited[i]) return vector<int>();
}
return ans;
}
};
|
DFS
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
|
// https://github.com/marcelklehr/toposort
/**
* Topological sorting function
*
* @param {Array} edges
* @returns {Array}
*/
module.exports = function(edges) {
return toposort(uniqueNodes(edges), edges)
}
module.exports.array = toposort
function toposort(nodes, edges) {
var cursor = nodes.length
, sorted = new Array(cursor)
, visited = {}
, i = cursor
// Better data structures make algorithm much faster.
, outgoingEdges = makeOutgoingEdges(edges)
, nodesHash = makeNodesHash(nodes)
// check for unknown nodes
edges.forEach(function(edge) {
if (!nodesHash.has(edge[0]) || !nodesHash.has(edge[1])) {
throw new Error('Unknown node. There is an unknown node in the supplied edges.')
}
})
while (i--) {
if (!visited[i]) visit(nodes[i], i, new Set())
}
return sorted
function visit(node, i, predecessors) {
if(predecessors.has(node)) {
var nodeRep
try {
nodeRep = ", node was:" + JSON.stringify(node)
} catch(e) {
nodeRep = ""
}
throw new Error('Cyclic dependency' + nodeRep)
}
if (!nodesHash.has(node)) {
throw new Error('Found unknown node. Make sure to provided all involved nodes. Unknown node: '+JSON.stringify(node))
}
if (visited[i]) return;
visited[i] = true
var outgoing = outgoingEdges.get(node) || new Set()
outgoing = Array.from(outgoing)
if (i = outgoing.length) {
predecessors.add(node)
do {
var child = outgoing[--i]
visit(child, nodesHash.get(child), predecessors)
} while (i)
predecessors.delete(node)
}
sorted[--cursor] = node
}
}
function uniqueNodes(arr){
var res = new Set()
for (var i = 0, len = arr.length; i < len; i++) {
var edge = arr[i]
res.add(edge[0])
res.add(edge[1])
}
return Array.from(res)
}
function makeOutgoingEdges(arr){
var edges = new Map()
for (var i = 0, len = arr.length; i < len; i++) {
var edge = arr[i]
if (!edges.has(edge[0])) edges.set(edge[0], new Set())
if (!edges.has(edge[1])) edges.set(edge[1], new Set())
edges.get(edge[0]).add(edge[1])
}
return edges
}
function makeNodesHash(arr){
var res = new Map()
for (var i = 0, len = arr.length; i < len; i++) {
res.set(arr[i], i)
}
return res
}
|
第十三讲 哈夫曼树
HTTP2 使用 HPACK 压缩协议来了压缩 Header, 其主要包括三个部分
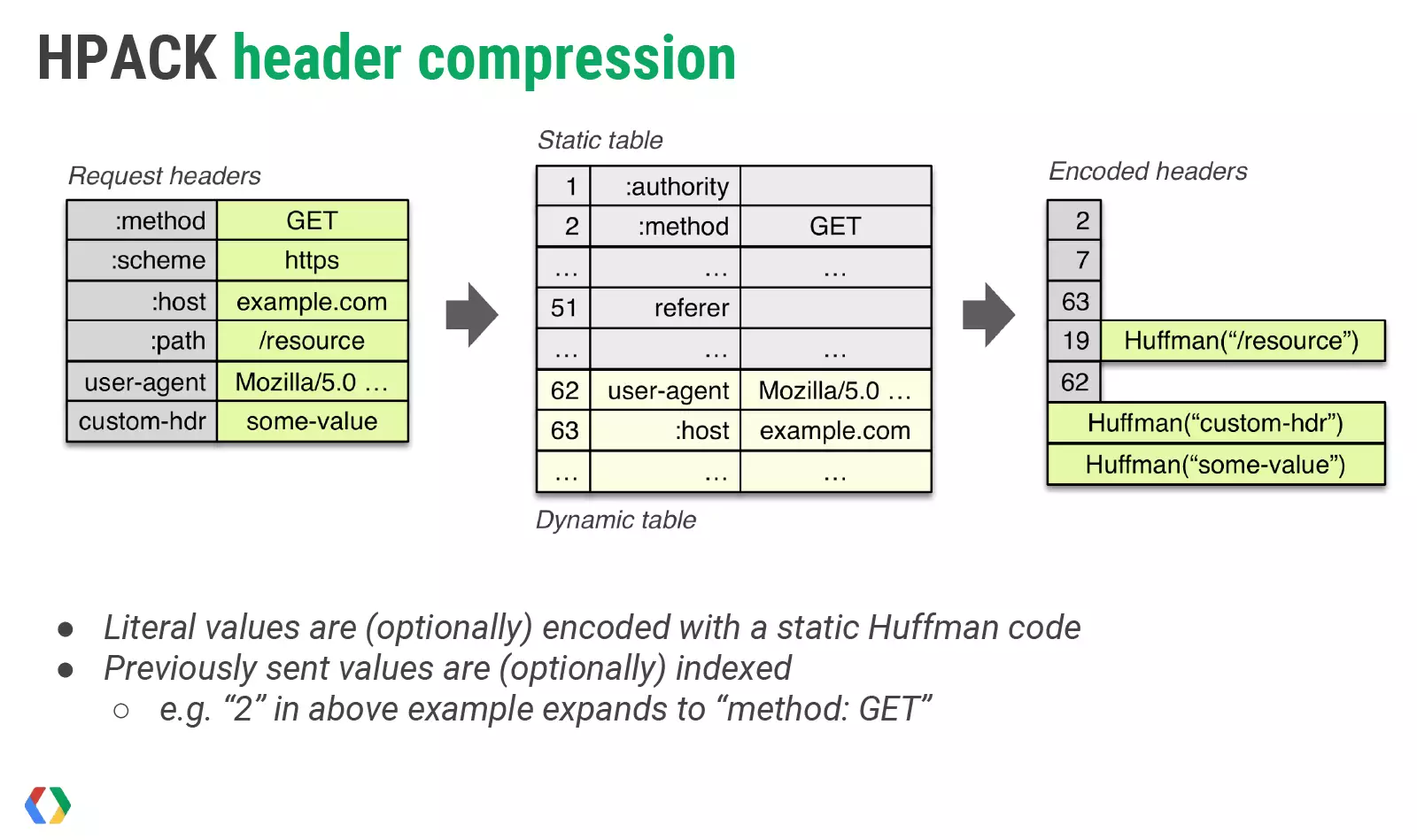
静态表
有 61 个 常用 字段(部分包含值)编码到了 1~61 的索引表里
动态表
静态表字段有限,允许通过通信的方式,在客户端和服务端之间维护一张动态的字典,用索引来代表值
哈夫曼编码
限于静态表和动态表的大小,我们并不能压缩任意数据,于是引入哈夫曼编码来进一步提高压缩能力 。
哈夫曼编码的主要思想就是让出现概率高的字符用短编码,概率低的用长编码;
同时为了避免变长编码产生歧义,所以不同的字符键不能成为对方的前缀。
算法实现采用了贪心思想,用一颗二叉树来标记每个字符的编码方式,左分支代表 0, 右分支代表 1;
所有需要编码的字符对应一个叶子节点,根节点到该叶子节点的路径代表该字符的编码方式。
编码示例,假设有 a、b、c、d、e、f 六个字符,分别出现的频率是 5、9、12、13、16、45。依次选取两个频率最小的节点合成一颗子树,用两个频率只和代表父节点的频率。
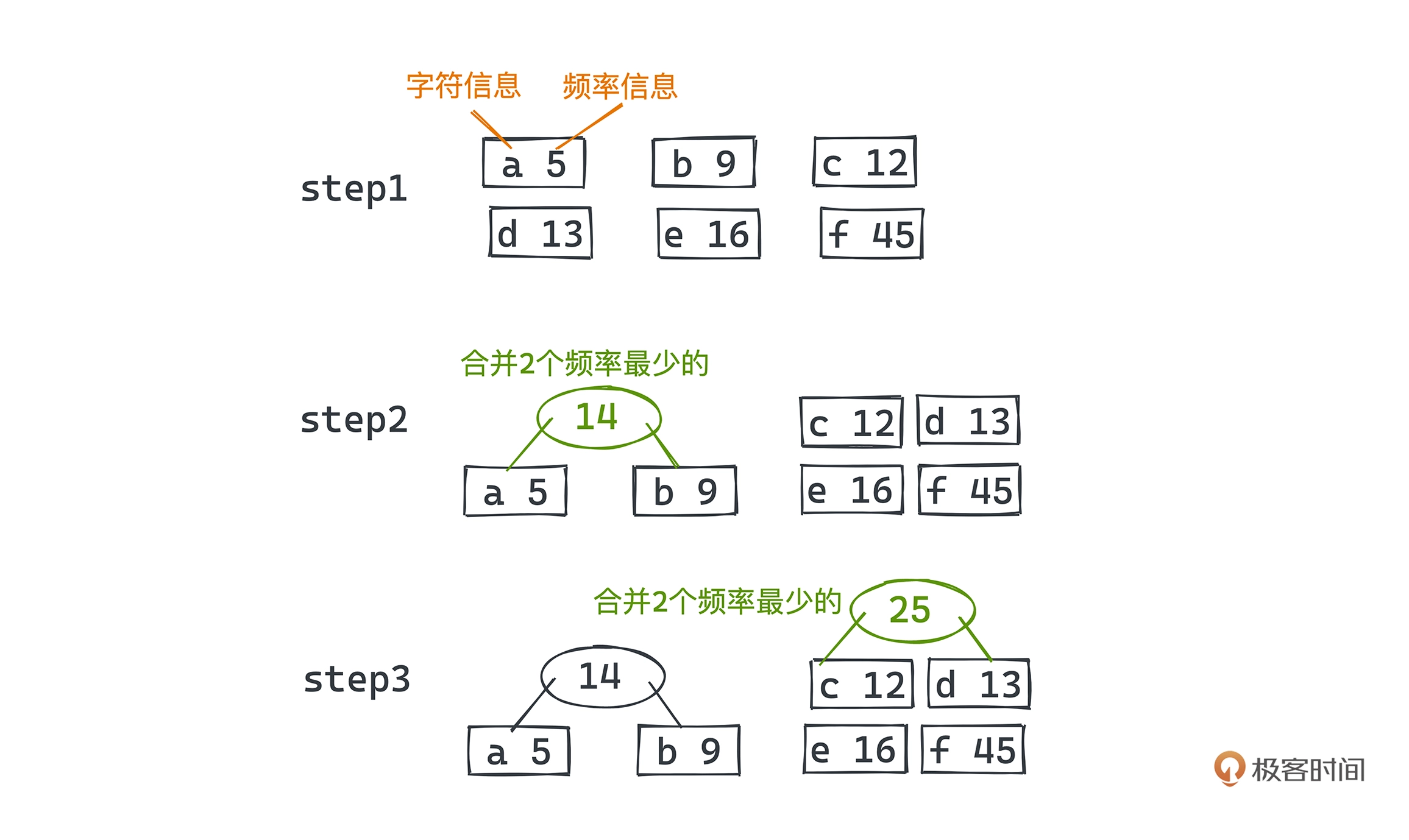
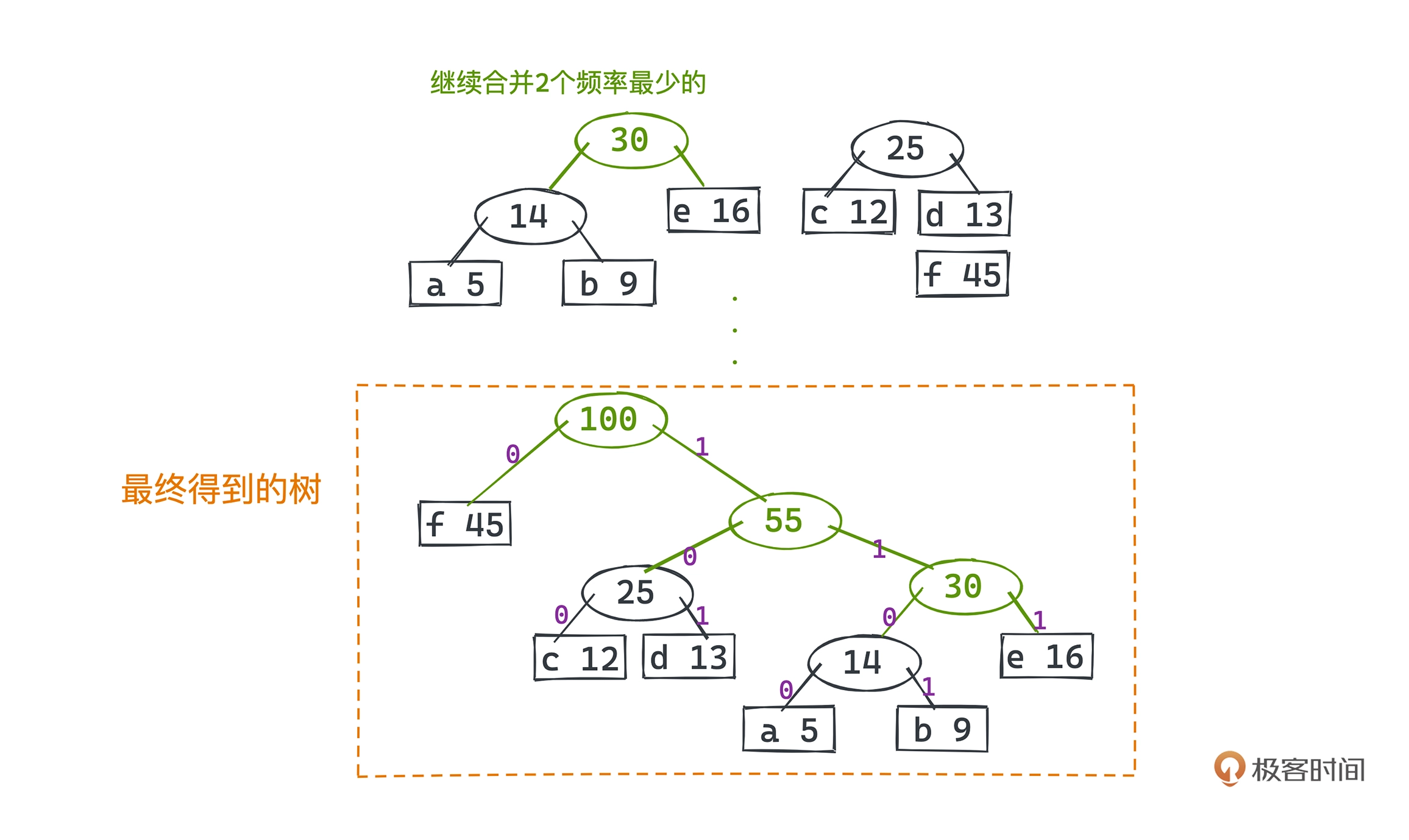
最终对应编码为:
1
2
3
4
5
6
|
f 0
c 100
d 101
a 1100
b 1101
e 111
|
代码实现可借助小顶堆
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
void buildHuffmanTree(string text)
{
// 利用hashmap对字符串进行频率计数
unordered_map<char, int> freq;
for (char ch: text) {
freq[ch]++;
}
// 用堆去动态维护所有树中最小的两颗
priority_queue<Node*, vector<Node*>, comp> pq;
// 将所有的字符都初始化成为哈夫曼树的一个叶子节点
// 并推入优先队列
for (auto pair: freq) {
pq.push(getNode(pair.first, pair.second, nullptr, nullptr));
}
// 每次取出最小的两个合并 直至优先队列只剩一个节点
while (pq.size() != 1)
{
// 最小的两个节点出队
Node *left = pq.top(); pq.pop();
Node *right = pq.top(); pq.pop();
// 建立一个内部节点,以这两个最小的树为左右节点
int sum = left->freq + right->freq;
pq.push(getNode('\0', sum, left, right));
}
// 优先队列中最后一个元素为整棵树的根节点
Node* root = pq.top();
}
|











































